Канонические уравнения Гамильтона
В силу известных свойств преобразования Лежандра имеем:
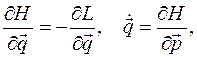
а из уравнений Лагранжа второго рода имеем 
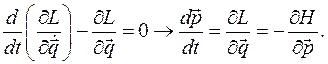
Тогда в переменных Гамильтона 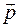 ,
, 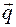 канонические уравнения Гамильтона запишутся так:
канонические уравнения Гамильтона запишутся так:
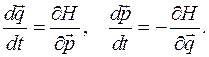
Уравнения Раусса.
Выберем теперь в качестве независимых переменных K обобщенных координат и обобщенных скоростей 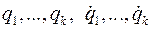 (их обозначение общего члена есть
(их обозначение общего члена есть 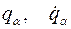 ) и n - k переменных
) и n - k переменных 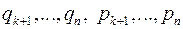 (их общий член обозначим
(их общий член обозначим 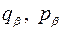 ).
).
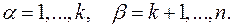
Определение. Функцией РаусаR называется преобразование Лежандра (со знаком минус) функции Лагранжа L по части обобщенных скоростей 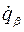 :
:
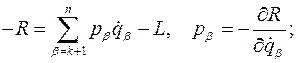
В переменных Раусса дифференциальные уравнения движения запишем в виде, который называется уравнениями Раусса:
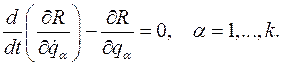
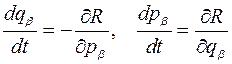
Доказательство. По свойству преобразования Лежандра имеем
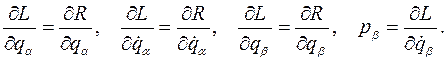
а по определению преобразования Лежандра и его свойству, а также по свойству двойного преобразования Лежандра имеет место
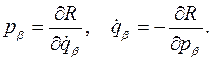
Наконец, из уравнения Лагранжа
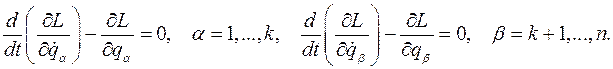
Следует
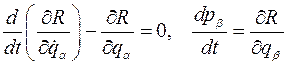
В результате, уравнения Раусса запишутся в виде.
Решение уравнений Раусса для систем с циклическими координатами.
Пусть теперь механическая система с n степенями свободы имеет циклические координаты 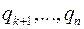 (их общее обозначение
(их общее обозначение 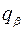 )
)
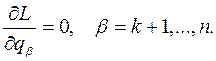
тогда как остальные координаты 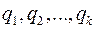 (позиционные координаты, их общее обозначение
(позиционные координаты, их общее обозначение 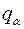 ) содержатся в функции Лагранжа
) содержатся в функции Лагранжа
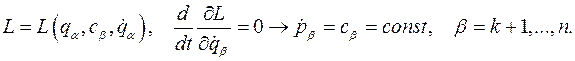
Если выполняется условие
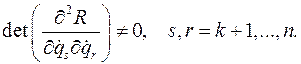
то из системы уравнений
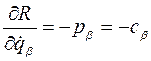
можно найти 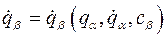 .
.
Зависимость позиционных координат от времени и начальных условий находят из первых уравнений Раусса
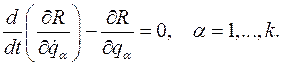
после чего из оставшихся уравнений ищут зависимость от времени позиционных координат.
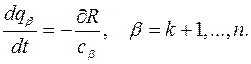
Дата добавления: 2020-05-20; просмотров: 738;











