Понятие устойчивости движений.

Изучается устойчивость некоторого множества решений 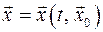уравнений движения консервативных систем, для которых начальные условия 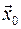находятся в малой окрестности некоторого положения равновесия системы, то есть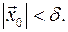

Определение. Решение уравнений движения консервативной системы 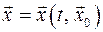называется устойчивым,если

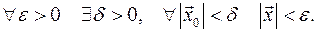
Устойчивое решение называется асимптотически устойчивым, если

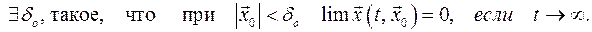
Далее для решения некоторых задач по устойчивости движений голономных систем будут использоваться достаточные условия устойчивости некоторых классов движений.

Достаточные условия устойчивости локальных положений равновесия консервативных систем. Теорема Дирихле – Лагранжа.

Пусть в консервативной системе нет циклических координат и существуют локальные (изолированные) положения равновесия, которые можно найти из условий экстремальности потенциальной энергии 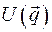в положении равновесия:

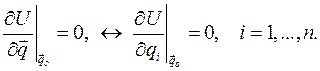
Теорема Дирихле - Лагранжа. Если в положении равновесия 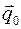потенциальная энергия консервативной системы имеет локальный минимум, то положение равновесия устойчиво по Ляпунову (по обобщенным координатам и скоростям).

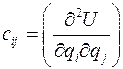Минимум потенциальной энергии U в положении равновесия определяется положительной определенностью матрицы из коэффициентов второго дифференциала потенциальной энергии . Часто критерия Сильвестра достаточно, чтобы проверить положительную определенность матрицы С: все главные миноры матрицы должны быть положительны.