Анализ уравнения Ленгмюра
Рассмотрим насколько хорошо описывает уравнение Ленгмюра изотерму адсорбции на всех ее участках.
На изотерме адсорбции, изображенной на рис. 3.10 можно выделить три участка. При малых значениях 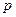 всегда можно подобрать такое значение
всегда можно подобрать такое значение 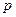 , когда значение
, когда значение 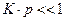 , и уравнение Ленгмюра принимает вид:
, и уравнение Ленгмюра принимает вид:
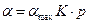 ,
,
То есть 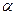 пропорциональна
пропорциональна 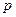 , что соответствует начальному линейному участку кривой. При больших значениях
, что соответствует начальному линейному участку кривой. При больших значениях 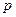 можно подобрать такие значения
можно подобрать такие значения 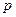 , когда величина
, когда величина 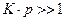 и
и 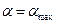 , что соответствует третьему участку изотермы. Второй криволинейный участок изотермы описывается полным уравнением Ленгмюра. Таким образом, это уравнение хорошо описывает всю изотерму адсорбции, в отличие от уравнения Фрейндлиха.
, что соответствует третьему участку изотермы. Второй криволинейный участок изотермы описывается полным уравнением Ленгмюра. Таким образом, это уравнение хорошо описывает всю изотерму адсорбции, в отличие от уравнения Фрейндлиха.
Существует два способа графического решения уравнения Ленгмюра (рис 3.14).
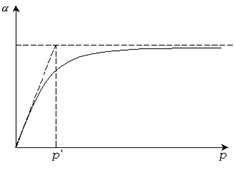
Рис. 3.14. Решение уравнения Ленгмюра.
По первому способу по изотерме находят значение 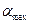 . Затем продолжают начальный прямолинейный участок изотермы до пересечения с линией
. Затем продолжают начальный прямолинейный участок изотермы до пересечения с линией 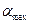 и из точки пересечения опускают перпендикуляр до точки
и из точки пересечения опускают перпендикуляр до точки 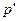 на оси абсцисс. При малых
на оси абсцисс. При малых 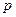 значение
значение 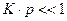 , и им знаменателе можно пренебречь. Тогда уравнение принимает вид:
, и им знаменателе можно пренебречь. Тогда уравнение принимает вид: 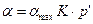 . При
. При 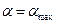
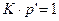 . Отсюда
. Отсюда 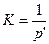 .
.
Второй способ решения уравнения Ленгмюра применяется, когда экспериментальная изотерма не имеет третьего линейного участка, т. е. значение 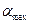 неизвестно. Уравнение преобразуется в уравнение прямой:
неизвестно. Уравнение преобразуется в уравнение прямой:
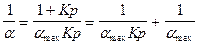 ;
; 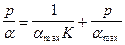 ;
;
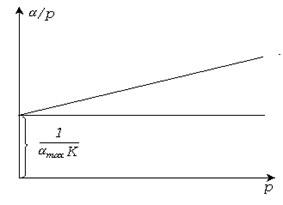
Рис.3.15. Решение уравнения Ленгмюра 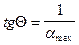 ;
; 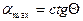
Уравнение Ленгмюра позволяет определить удельную поверхность адсорбента.
Действительно, произведение 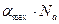 равно числу молекул, приходящихся на 1 см2 поверхности. Умножив это значение на площадь, занимаемую одной молекулой
равно числу молекул, приходящихся на 1 см2 поверхности. Умножив это значение на площадь, занимаемую одной молекулой 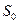 получим величину удельной поверхности
получим величину удельной поверхности 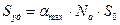 .
.
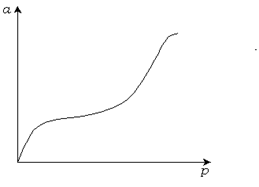
Рис. 3.16. Изотерма полимолекулярной адсорбции.
Часто изотермы адсорбции имеют вид, отличающийся от ленгмюровской изотермы, а именно 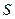 -образный вид (Рис. 3.16). Это объясняется полимолекулярной адсорбцией, или капиллярной конденсацией. Изотермы адсорбции полимеров, как правило, не являются ленгмюровскими, т. к. одна макромолекула занимает несколько активных центров адсорбента, т. е. предпосылки, положенные в основу уравнения Ленгмюра, не соблюдаются.
-образный вид (Рис. 3.16). Это объясняется полимолекулярной адсорбцией, или капиллярной конденсацией. Изотермы адсорбции полимеров, как правило, не являются ленгмюровскими, т. к. одна макромолекула занимает несколько активных центров адсорбента, т. е. предпосылки, положенные в основу уравнения Ленгмюра, не соблюдаются.
Дата добавления: 2020-11-18; просмотров: 1294;











