Малые колебания обобщенно -- консервативных систем около относительных положений равновесия.

В равномерно вращающейся системе отсчета теория аналогична теории малых колебаний консервативных систем, только вместо потенциальной энергии U нужно взять обобщенную потенциальную энергию 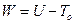, а вместо кинетической энергии T взять ее квадратичную часть .

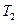Малые колебания консервативных систем с циклическими координатами около стационарных движений и безразличных положений равновесия.

Используем функцию Раусса для приведенной системы и рассмотрим ее представление

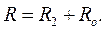
Функция 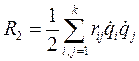есть положительно определенная форма позиционных скоростей с коэффициентами, зависящими от позиционных координат.

Перейдем к квадратичной форме с постоянными коэффициентами

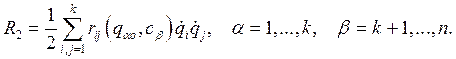
Заменим функцию 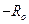квадратичной формой

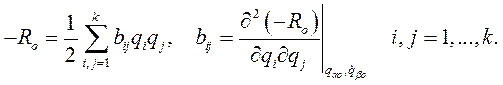
Тогда из первых n уравнений системы линейных уравнений получим уравнения малых колебаний системы около стационарного движения.

Метод нахождения малых колебаний в это случае аналогичен методу для консервативных систем.