Функции Гамильтона и Раусса. Уравнения Гамильтона и Раусса.
Введемфункцию Лагранжа 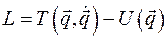 =
= 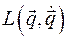 , записанную в переменных Лагранжа, Так как для консервативной и обобщенно консервативной систем в кинетической энергии системы имеется квадратичная функция обобщенных скоростей
, записанную в переменных Лагранжа, Так как для консервативной и обобщенно консервативной систем в кинетической энергии системы имеется квадратичная функция обобщенных скоростей
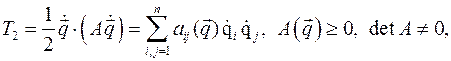
то 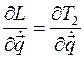 линейно зависит от обобщенных скоростей. Применим к функции Лагранжа преобразование Лежандра по обобщенным скоростям:
линейно зависит от обобщенных скоростей. Применим к функции Лагранжа преобразование Лежандра по обобщенным скоростям:
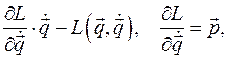
где 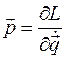 есть обобщенный импульс. Так как матрица A положительно определена, из этой системы линейных уравнений относительно обобщенных скоростей выразим обобщенные скорости через обобщенные импульсы и обобщенные координаты. В результате, подставляя обобщенные скорости в функцию
есть обобщенный импульс. Так как матрица A положительно определена, из этой системы линейных уравнений относительно обобщенных скоростей выразим обобщенные скорости через обобщенные импульсы и обобщенные координаты. В результате, подставляя обобщенные скорости в функцию
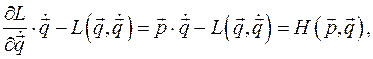
мы выражаем ее через новые переменные 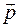 ,
, 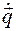 , которые называются переменными Гамильтона.
, которые называются переменными Гамильтона.
Определение. Функция 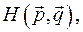 результат преобразования Лежандра функции Лагранжа по обобщенным скоростям
результат преобразования Лежандра функции Лагранжа по обобщенным скоростям 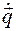 , называется функцией Гамильтона:
, называется функцией Гамильтона:
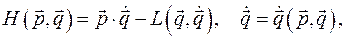
В частности, для консервативной системы функция Лагранжа имеет следующий вид:
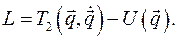
Из системы линейных уравнений 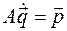 обобщенные скорости выражаются просто:
обобщенные скорости выражаются просто: 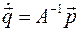 .
.
Дата добавления: 2020-05-20; просмотров: 717;











