Дифференциальные уравнения движения голономных систем. Уравнения Лагранжа второго рода.

В голономной механической системе наложенные на систему связи есть геометрические связи или кинематические связи, сводящиеся к геометрическим их интегрированием. Число независимых параметров, обобщенных координат, задающих положение системы, равно числу степеней свободы и числу независимых вариаций координат в уравнениях связей в вариациях.

Рассмотрим далее голономную систему N твердых тел с 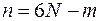степенями свободы и с m уравнениями геометрических идеальных связей.

Дифференциальный принцип механики для таких систем имеет вид:

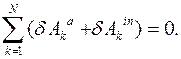
Это уравнение эквивалентно n скалярным уравнениям, которые можно представить в виде уравнений Лагранжа.

Для их вывода необходимо понятие кинетической энергии твердого тела и системы тел.

Кинетическая энергия твердого тела.

Пусть вектор 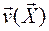задает поле абсолютных скоростей элементарных масс (точек) движущегося тела, положение которых в системе координат, жестко связанной с телом, и с началом в центре масс, задается векторами 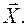Определение.Кинетическая энергия твердого тела в любом его положении определяется как совокупность кинетических энергий элементарных масс тела :

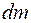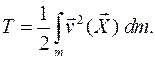
Задавая массовую плотность любой элементарной массы тела этот интеграл можно представить как тройной интеграл по объему тела.

Так как 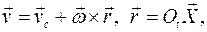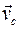и 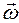есть абсолютная скорость центра масс и абсолютная угловая скорость тела, то кинетическая энергия тела может быть представлена в виде двух слагаемых:

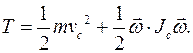
Здесь 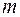есть масса тела, 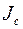есть оператор инерции тела относительно осей, связанных с телом, с началом в его центре масс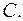

Доказательство:

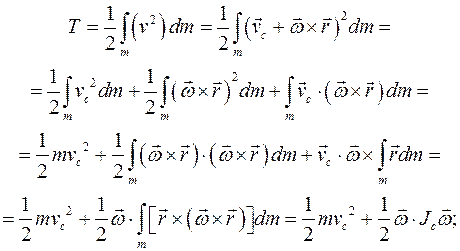
Если в теле есть неподвижная точка 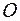, то кинетическая энергия тела вычисляется по формуле:

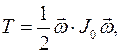
где 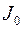есть оператор инерции тела относительно точки 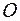. В главных осях оператора инерции его матрица имеет только диагональные осевые моменты инерции 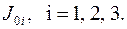Поэтому в главных осях