Нормальное распределение
Закон распределения вероятностей непрерывной случайной величины Х называется нормальным, если ее дифференциальная функция f (x) определяется формулой: 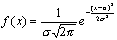
где а совпадает с математическим ожиданием величины Х: а = М(Х), параметр a совпадает со средним квадратическим отклонением величины Х: σ = σ (Х).
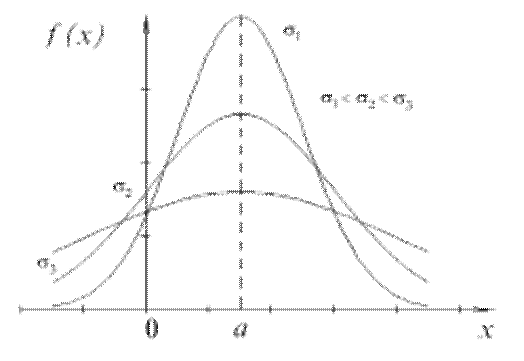
График функции нормального распределения, как видно из рисунка, имеет вид куполообразной кривой, называемой Гауссовой, точка максимума имеет координаты (а; 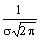 ). Значит, эта ордината убывает с возрастанием значения s (кривая "сжимается" к оси Ох) и возрастает с убыванием значения s (кривая "растягивается" в положительном направлении оси Оу). Изменение значений параметра а (при неизменном значении s) не влияет на форму кривой, а лишь перемещает кривую вдоль оси Ох.
). Значит, эта ордината убывает с возрастанием значения s (кривая "сжимается" к оси Ох) и возрастает с убыванием значения s (кривая "растягивается" в положительном направлении оси Оу). Изменение значений параметра а (при неизменном значении s) не влияет на форму кривой, а лишь перемещает кривую вдоль оси Ох.
Нормальное распределение с параметрами а = 0 и σ = 1 называется нормированным. Дифференциальная функция в случае такого распределения будет:
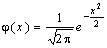
Пусть случайная величина Х распределена по нормальному закону. Тогда вероятность того, что Х примет значение, принадлежащее интервалу (a; b)
Пример 1.Бросаются две правильные однородные монеты. Сколько из них выпадает гербом кверху?
При подбрасывании двух монет пространство элементарных событий имеет вид:
U = {ЦЦ,ЦГ,ГЦ,ГГ}, где Ц- «цифра», Г- «герб».
Первый символ показывает, как выпала первая монета, а второй - вторая монета. Например, ЦГ означает, что первая монета выпала цифрой кверху, а вторая - гербом. Так как монеты правильные и однородные, то можно считать, что все элементарные события пространства U равновероятны, и тогда вероятность каждого из них равна %. Обозначим через X число монет, выпавших гербом кверху, составим таблицу:
| U | ЦЦ | ЦГ | ГЦ | ГГ |
| X | 0 | 1 | ||
| р | 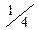
| 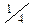
| 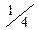
| 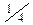
|
Так как элементарным событиям ЦГ и ГЦ соответствует одно и то же значение величины Х, равное 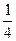 , то можно полагать, что это значение величина X принимает с 4х вероятностью. Таким образом, значение величины X - число монет, выпавших гербом кверху и соответствующие им вероятности можно записать в виде таблицы.
, то можно полагать, что это значение величина X принимает с 4х вероятностью. Таким образом, значение величины X - число монет, выпавших гербом кверху и соответствующие им вероятности можно записать в виде таблицы.
| X | 2 | ||
| р | 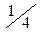
| 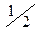
| 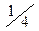
|
Итак, каждое значение величины X есть число, определяемое исходом опыта и зависящее от случая.
Определение 1.Случайной называется величина, которая в результате опыта принимает с определенной вероятностью, то или иное значение, зависящее от исхода опыта. Случайные величины обозначают прописными буквами латинского алфавита: X, Y, Z и т.д., а их значения - соответствующими буквами : х, у, z и т.д.,
Определение 2.Случайная величина называется дискретной, если множество её значений конечно или счётно, т.е. множество её значений представляет собой конечную последовательность х],х2,х3,...,хп. Вероятность того, что случайная величина X примет значение х, обозначают Р{х) = Р(Х = х)
Определение 3.Соответствие между возможными значениями xvx2,...,xn случайной величины X и их вероятностями pvp2,—,Pn называется законом распределения случайной величины X.
Закон распределения случайной величины может быть представлен в виде таблицы:
| X | х 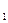
| х2 | ... | х 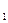
| ... | Х 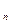
|
| р | Р1 | P2 | ... | Pi | ... | Рп |
События X = xv X = х2,...,Х = хп образуют полную систему попарно несовместных событий, поэтому сумма их вероятностей равна единице р1 + р2 +... + рп = 1.
Пример 2.Закон распределения вероятностей случайной дискретной величины Х- числа очков, выпадающих при бросании правильной игральной кости, имеет вид, заданный таблицей:
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| р | 1 6 | 1 6 | 1 6 | 1 6 | 1 6 | 1 6 |
2. Биноминальное распределение случайной дискретной величины.
Пусть случайная величина Х- число появлений события А в п независимых испытаниях, в каждом из которых вероятность появления событий А равно р , а непоявления - q = 1-р. Очевидно, что Сможет принимать значения 0,1,2,..., п, вероятности которых определяются по формуле Бернулли:
Рп(т) = Р(Х = т) = С 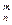 *рт -qn m, m = 0,1,2,..., и. (1)
*рт -qn m, m = 0,1,2,..., и. (1)
Определение. Закон распределения случайной величины X, имеющий вид:
| X | 0 | 1 | 2 | т | п | ||
| р | C 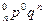
| С 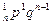
| C 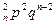
| ... | С 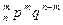
| C 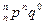
|
называется биноминальным распределением.
Пример 3.Составить закон распределения числа попаданий в цель при четырёх выстрелах, если вероятность попадания при одном выстреле равна 0,9.
Случайная величина Х- число попаданий в цель при четырёх выстрелах - может принимать значения 0,1,2,3,4, а соответствующие им вероятности находим по формуле Бернулли (2):
P(Х = 0) = С4° • 0,9° • О,14 = 0,0001;
Р(Х = 1) = С 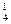 •0,9 • 0,13 = 0,0036;
•0,9 • 0,13 = 0,0036;
Р(Х = 2) = С 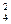 •0,92 • О,12 = 0,0486;
•0,92 • О,12 = 0,0486;
Р(Х = 3) = С 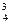 •0,93 • О,1 = 0,2916;
•0,93 • О,1 = 0,2916;
P(Х = 4) = С44 • 0,94 • 0,1° = 0,6561;
Итак, искомый закон распределения имеет вид.
| X | 0 | 1 | 2 | ||
| р | 0,0001 | 0,0036 | 0,486 | 0,2916 | 0,6561 |
Пример 4. В ОТК измерялась длина в мм у 50 деталей, изготовленных на одном станке – автомате. В результате измерений получены следующие данные:
Требуется произвести первичную статистическую обработку данных:
1) Составить статистический ряд распределения частот и относительных частот длины деталей (случайная величина Х)
2) построить полигоны частот и относительных частот
3) найти эмпирическую функцию распределения и построить ее график
РЕШЕНИЕ:
1) Для составления статистических рядов исходные данные располагаются в порядке возрастания, затем подсчитываются частоты ni и относительные ni/n появление каждого из наблюдаемых значений (n=50).
| Наблюдаемые значения | |||||||
| Подсчет частоты | |||||||
| Относительные частоты | 0,08 | 0,1 | 0,2 | 0,28 | 0,16 | 0,08 | 0,1 |
2) Изобразим полигон частот и относительных частот
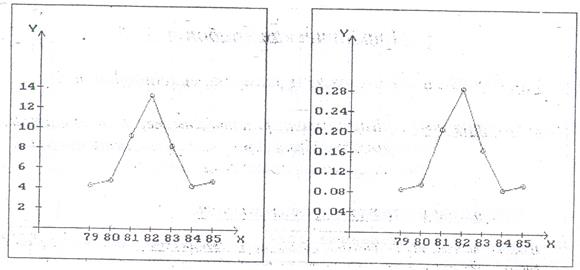
3) Эмпирическая функция распределения F*(x) определяется как отношение накопленных частот n*, т.е числа выборочных значений меньших х, объему выборки n.
| При х ≤ 79, | nx = 0, | F*(x) = 0/50 = 0 |
| При 79 < x ≤ 80, | nx = 4, | F*(x) = 4/50 = 0,08 |
| При 80 < x ≤ 81, | nx = 4+5=9, | F*(x) = 9/50 = 0,18 |
Аналогично вычисляются значения F*(x) на других интервалах.
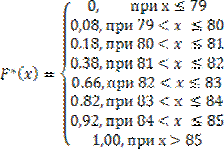
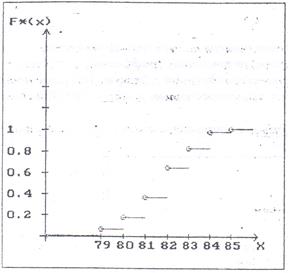
График функции F*(x):
Лекция 12. Математическое ожидание дискретной случайной величины. Дисперсия случайной величины. Среднее квадратное отклонение случайной величины
Дата добавления: 2020-05-20; просмотров: 738;











