Свойства вероятности

Суммой событий A и B называется событие C = A + B, состоящее в наступлении, по крайней мере, одного из событий - A или B.

Теорема. Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий: P (A + B) = P(A) + P(B).

Примеры: пусть А - идет дождь, а В - идет снег, то (А + В) - либо дождь, либо снег, либо дождь со снегом, т. е. осадки; А - пошли на дискотеку; В - пошли в библиотеку, то А + В - пошли либо на дискотеку, либо в библиотеку, т. е. вышли из дома.

Следствие. Сумма вероятностей противоположных событий А и равна единице:

P(A) + P = 1.

Вероятность суммы полной группы событий равна 1.

Примеры: если А - число четное, то - число нечетное; если А - зима, то - не зима (либо осень, либо лето, либо весна); если А - сдал экзамен, то –

не сдал экзамен.

Произведением событий А и В называется событие С = АВ, состоящее в том, что в результате испытания произошло и событие А и событие В.

Примеры: пусть А - из урны вытянули белый шар, В - из урны вытянули белый шар, то АВ - из урны вытянули два белых шара; А - идет дождь, В - идет снег, то АВ – дождь со снегом; А - число четное, В - число кратное 3, то АВ - число кратное 6.

Два события A и B называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события A и B называются зависимыми.

Чаще всего зависимые испытания происходят тогда, когда тянут из одной колоды, не возвращая карты в колоду, вытаскивают из одной урны и т.д.

Теорема. Вероятность произведения двух независимых событий A и B равна произведению их вероятностей:

P(AB) = P(A) P(B).

Пусть А и В - зависимые. Условной вероятностью PA (B) события В называется вероятность события В, найденная в предположении, что событие А уже наступило.

Теорема. Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:

P (AB) = P (A) PА (B).

Теорема. Вероятность суммы двух совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения

P (A + B) = P (A) + P (B) - P (AB).

Теорема (формула полной вероятности). Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместных событий B₁, B₂,…, B_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:

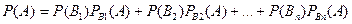
Теорема (формула Байеса). Если существуют n попарно несовместных событий B₁, B₂, …, B_n, образующих полную группу, и известны условные вероятности события А, то можно найти вероятности того, что событие А произошло при условии появления некоторого события B_k по формуле:

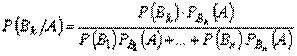
Лекция 11. Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения случайной величины.

Если результатом испытания является случайное событие, принимающее числовое значение, то говорят о случайной величине.

Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.

Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной случайной величиной. Примеры: число очков, выпавших при бросании игральной кости; число родившихся детей в семье; число шаров, которые можно достать из урны и т. д.

Случайная величина, которая может принимать все значения из некоторого числового промежутка, называется непрерывной случайной величиной.

Примеры: прирост веса домашнего животного за месяц есть случайная величина, которая может принять значение из некоторого промежутка; прогнозируемая температура воздуха по области и т. д.