Характеристики случайной величины
1. Математическое ожидание
Кроме закона распределения, который даёт полное представление о случайной величине, часто используют числа, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины. Среди числовых характеристик весьма важной является математическое ожидание,которое указывает, какое среднее значение случайной величины следует ожидать в результате испытаний или наблюдений.
Определение 1.Математическим ожиданием М(Х) дискретной случайной величины X называется сумма произведений всех её возможных значений х, на их вероятности pi:
М(Х) = ххрх +х2р2+... + х„р„ = 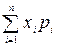
Пример 1.Найти математическое ожидание М(Х) случайной величины X, зная закон её
распределения.
| X | -1 | 0 | 1 | 2 | 3 |
| р | 0,2 | 0,1 | 0,25 | 0,15 | 0,3 |
Решение: по формуле (1) находим
М(Х) = -1*0,2 + 0*0.1 + 1*0,25 + 2*0,15 + 3*0,3 =1,25. Приведём без доказательства свойства математического ожидания:
1. Постоянный множитель можно выносить за знак математического ожидания:
M(CX)=CM(X)
2. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий (теорема математических ожиданий):
М(Х + Y) = М(Х) + M(Y).
3. Математическое ожидание постоянной величины С равно самой этой величине:
М(С)=С
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий (теорема умножения математических ожиданий):
m(xy)=m(x)-m(y).
Пример 2.Куплено 100 лотерейных билетов, причем на каждый из 10 билетов выпал выигрыш в 50 руб., 5 билетов -100 руб. 2 билета -300руб. Найти средний выигрыш, выпавший на один
билет.
Решение: введём случайную величину Х- размер выигрыша. Тогда эта случайная величина принимает следующие значения х, = 0, х2 = 50, х3 = 100, х4 = 300, а вероятность того,
что р(Х = 50) = 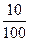 = 0,1; р(Х = 100) =
= 0,1; р(Х = 100) = 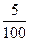 = 0,05; р(Х = 300) =
= 0,05; р(Х = 300) = 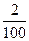 = 0,02 и значит
= 0,02 и значит
р(Х = О) = 1 - 0,1 - 0,05 - 0,02 = 0,83. Значит случайная величина X имеет закон распределения:
| х | ||||
| Pi | 0,83 | О,1 | 0,05 | 0,02 |
Тогда средний выигрыш выпавший на один билет есть М (X), поэтому
М(х) = 0 • 0,83 + 50 • 0,1 +100 • 0,05 + 300 • 0,02 = 16(руб).
2.Дисперсия случайной величины.
Рассмотрим следующий пример.
Пример 3. Найти математическое ожидание случайных величиной Y, зная законы их распределения.
| X | -8 | -4 | L -1 | 1 | 3 | 7 |
| р | 1/ 12 | 1 /6 | 1/4 | 1/ 6 | 1/12 | 1/ 4 |
| Y | -2 | -1 | 0 | 1 | 2 | 3 |
| Р | 1/ 6 | 1 /6 | 1/12 | 1/3 | 0 | 1/4 |
По формуле (1) имеем М(х) = 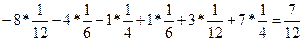
M(y) = 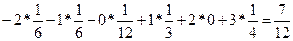
Мы получили любопытный результат: законы распределения величиной Г разные, а их математические ожидания одинаковы.
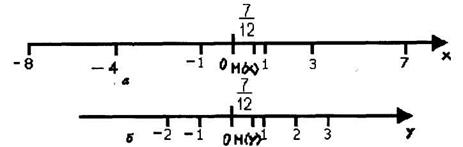
Из рисунка видно, что значения величины Y более сосредоточены около математического ожидания М(У), чем значения величины X, которые разбросаны относительно ее математического ожидания М(х).
Основной числовой характеристикой степени рассеяния значений случайной величины X относительно ее математического ожидания М(х) является дисперсия, которая обозначается через D(X).
Определение 2. Отклонением называется разность между случайной величиной X и ее математическим ожиданием Х-М(х).
Заметим, что отклонение X - М(х) и его квадрат (X - M(x))2 также являются случайными величинами. Причем если X случайная величина распределена по закону,
| X | ||||
| р | Р\ | Pi | ... | Рп |
то квадрат её" отклонения имеет следующий закон распределения
| (x-M(x)f | (х,-м(х)У | (х2-м(х)У | (xn-M(X)f | |
| р | P1 | Рг | Рп |
Введём теперь определение дисперсии случайной величины X.
Определение 3. Дисперсией случайной дискретной величины X называется математическое ожидание квадрата ее отклонения:
D(X) = M(X - M(x)2) (2)
Приведем без доказательства некоторые свойства дисперсии.
Дисперсия постоянной величины С равна нулю: D(c) = О
Если Х- случайная величина, С - постоянная, то D(CX) = C2D(x) и D{X + С) = D(X)
Если X u Y- независимые случайные величины, то D(X + Y) = D(x) + D(Y)
Для вычисления дисперсий более удобной является формула
D(X)=M(X2)-M(X)Y (3)
Пример 4. Случайная дискретная величина распределена по закону
| X | -1 | |||
| р | 0,2 | од | 0,3 | 0,4 |
Найти: D(X).
Сначала находим М(х) = -1 • 0,2 + 0 • 0,1 +1 • 0,3 + 2 • 0,4 = 0,9, а затем
М(Х2)= 1-0,2 + 0-0,1 + 1-0,3 + 4- 0,4 = 2,1.
По формуле (3) имеем D(x) = м(х2)- М2 (X) = 2,1 - 0,81 = 1,29.
Пример 5. Сравнить дисперсии случайных величин Х и Y, заданных законами распределения
| X | -1 | |||
| р | 0,48 | 0,01 | 0,09 | 0,42 |
| Y | -1 | |||
| Р | 0,19 | 0,51 | 0,25 | 0,05 |
Находим
М(Х) = (-1) • 0,48 +1 • 0,01 + 2 • 0,09 + 3 • 0,42 = 0,97;
М(х2) = 1 * 0,48 +1 • 0,01 + 4 • 0,09 + 9 • 0,42 = 4,63;
D(X) = 4,63 -0,972 =3,69;
M(Y) = (-1)*0,19 +1 • 0,51 + 2 • 0,25 + 3 • 0,05 = 0,97
M(Y2)=1*0,19 +1*0,51+ 4*0,25+ 9*0,05 = 2,15;
D(Y) = 2,15 -0,972 =1,21.
Полученные результаты показывают, что несмотря на то, что значения и математические ожидания случайных величиной У одинаковы, их дисперсии различны, причем D(x)> D(y). Это означает, что случайная величина Y с большей вероятностью принимает значения, близкие к математическому ожиданию, чем случайная величина X.
Пример 6. Найти числовые характеристики (n = 50)
| Наблюдаемые значения | |||||||
| частоты |
1) Выборочное среднее
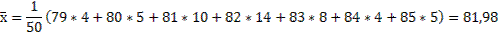
2) Выборочная дисперсия:
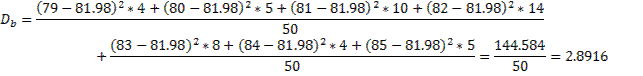
3) Выборочное среднее квадратическое отклонение:
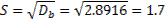
Биноминальное распределение случайной дискретной величины.
Пусть случайная величина Х- число появлений события А в п независимых испытаниях, в каждом из которых вероятность появления событий А равно р , а непоявления - q = 1-р. Очевидно, что Сможет принимать значения 0,1,2,..., п, вероятности которых определяются по формуле Бернулли:
Рп(т) = Р(Х = т) = С 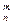 *рт -qn m, m = 0,1,2,..., и. (1)
*рт -qn m, m = 0,1,2,..., и. (1)
Определение. Закон распределения случайной величены X, имеющий вид:
| X | 0 | 1 | 2 | т | п | ||
| р | C 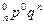
| С 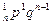
| C 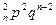
| ... | С 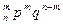
| C 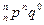
|
называется биноминальным распределением.
Пример 3.Составить закон распределения числа попаданий в цель при четырёх выстрелах, если вероятность попадания при одном выстреле равна 0,9.
Случайная величина Х- число попаданий в цель при четырёх выстрелах - может принимать значения 0,1,2,3,4, а соответствующие им вероятности находим по формуле Бернулли (2):
P(Х = 0) = С4° • 0,9° • 0,14 = 0,0001;
Р(Х = 1) = С 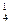 * 0,9 • 0,13 = 0,0036;
* 0,9 • 0,13 = 0,0036;
Р(Х = 2) = С 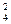 * 0,92 • 0,12 = 0,0486;
* 0,92 • 0,12 = 0,0486;
Р(Х = 3) = С 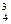 * 0,93 • 0,1 = 0,2916;
* 0,93 • 0,1 = 0,2916;
P(Х = 4) = С44 • 0,94 • 0,1° = 0,6561;
Итак, искомый закон распределения имеет вид.
| X | 0 | 1 | 2 | ||
| р | 0,0001 | 0,0036 | 0,486 | 0,2916 | 0,6561 |
Литературные и интернет – источники:
1. Письменный Д. Конспект лекций по высшей математике. http://rutracker.org/forum/viewtopic.php?t=756864
2. Лисичкин В.Т., Соловейчик И.Л. Математика. – М., Высшая школа, 2011.
3. Богомолов Н. В. Практические занятия по математике. - М., Высшая школа, 2003.
Дата добавления: 2020-05-20; просмотров: 844;











