Метод конечных разностей решения краевых задач для ОДУ

Постановка задачи: найти решение линейного дифференциального уравнения

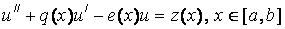, (1)

удовлетворяющего краевым условиям: 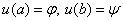. (2)

Теорема. Пусть 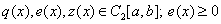. Тогда существует единственное решение поставленной задачи.

К данной задаче сводится, например, задача об определении прогибов балки, которая на концах опирается шарнирно.

Основные этапы метода конечных разностей:

1) область непрерывного изменения аргумента ([a,b]) заменяется дискретным множеством точек, называемых узлами: .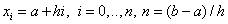

2) Искомая функция непрерывного аргумента x, приближенно заменяется функцией дискретного аргумента на заданной сетке, т.е. 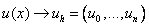. Функция 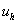называется сеточной.

3) Исходное дифференциальное уравнение заменяется разностным уравнением относительно сеточной функции. Такая замена называется разностной аппроксимацией.

Таким образом, решение дифференциального уравнения сводится к отысканию значений сеточной функции в узлах сетки, которые находятся из решения алгебраических уравнений.