Численные методы решения систем ОДУ первого порядка

Рассмотренные методы могут быть использованы также для решения систем дифференциальных уравнений первого порядка.

Покажем это для случая системы двух уравнений первого порядка:

Явный метод Эйлера:

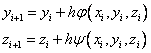
Модифицированный метод Эйлера:

Схема Рунге – Кутта четвертого порядка точности:

К решению систем уравнений ОДУ сводятся также задачи Коши для уравнений высших порядков. Например, рассмотрим задачу Коши для уравнения второго порядка

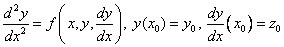
Введем вторую неизвестную функцию 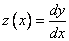. Тогда задача Коши заменяется следующей:

Т.е. в терминах предыдущей задачи: .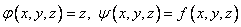

Пример. Найти решение задачи Коши:

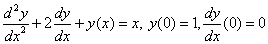на отрезке [0,1].

Точное решение: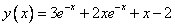

Действительно:

Решим задачу явным методом Эйлера, модифицированным методом Эйлера и Рунге – Кутта с шагом h=0.2.

Введем функцию .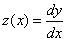

Тогда получим следующую задачу Коши для системы двух ОДУ первого порядка:

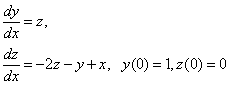
Явный метод Эйлера:

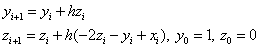
Модифицированный метод Эйлера:

Метод Рунге – Кутта:

Схема Эйлера:

X	y	z	y теор	z теор	y-y теор

0.2		-0.2	0.983685	-0.14622	0.016315
0.4	0.96	-0.28	0.947216	-0.20658	0.012784
0.6	0.904	-0.28	0.905009	-0.20739	0.001009
0.8	0.848	-0.2288	0.866913	-0.16826	0.018913
	0.80224	-0.14688	0.839397	-0.10364	0.037157

Модифицированный метод Эйлера:

X	ycv	zcv	y	z	y теор	z теор	y-y теор

0.2		-0.2		-0.18	0.983685	-0.14622	0.016315
0.4	0.96	-0.28	0.962	-0.244	0.947216	-0.20658	0.014784
0.6	0.904	-0.28	0.9096	-0.2314	0.905009	-0.20739	0.004591
0.8	0.848	-0.2288	0.85846	-0.17048	0.866913	-0.16826	0.008453
	0.80224	-0.14688	0.818532	-0.08127	0.839397	-0.10364	0.020865

Схема Рунге - Кутта:

x	Y	z	k1	l1	k2	l2	k3	l3	k4	l4
				-1	-0.1	-0.7	-0.07	-0.75	-0.15	-0.486
0.2	0.983667	-0.1462	-0.1462	-0.49127	-0.19533	-0.27839	-0.17404	-0.31606	-0.20941	-0.13004
0.4	0.947189	-0.20654	-0.20654	-0.13411	-0.21995	0.013367	-0.2052	-0.01479	-0.2095	0.112847
0.6	0.904977	-0.20734	-0.20734	0.10971	-0.19637	0.208502	-0.18649	0.187647	-0.16981	0.27195
0.8	0.866881	-0.16821	-0.16821	0.269542	-0.14126	0.332455	-0.13497	0.317177	-0.10478	0.369665
	0.839366	-0.1036	-0.1036	0.367825	-0.06681	0.40462	-0.06313	0.393583	-0.02488	0.423019