Определенный интеграл.

<5 6 789 10 11 >

Определение. Приращение F (b) - F (а) любой из первообразных функций F (х) + С функции f (х) при изменении аргумента от х = а до х = b называется определённым интегралом от а до b функции f(x) и обозначается: 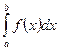(1)

Числа а и b называются пределами интегрирования, а - нижним, b - верхним. Отрезок [а;b] называется отрезком интегрирования. Функция f(x) называется подынтегральной функцией, а переменная х - переменной интегрирования.

Таким образом, по определению 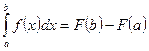(2)

Данное равенство называется формулой Ньютона - Лейбница.

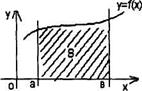
Геометрический смысл определенного интеграла:если интегрируемая на отрезке [а;b] функция f (х) неотрицательна, то определённый интеграл 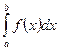численно равен площади S криволинейной трапеции, ограниченной графиком функции f (x), осью абсцисс и прямыми х = аих = b:

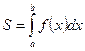
Пример 1:Вычислить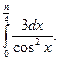

Решение:

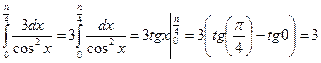
Пример 2: Вычислить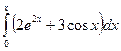

Решение: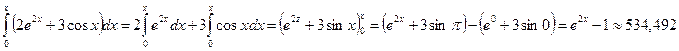

Методы вычисления определенного интеграла.

Непосредственное интегрированиепредполагает использование основных свойств определенного интеграла и формулы Ньютона - Лейбница.

Пример 3. Вычислить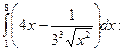

Решение: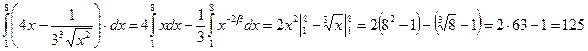

Метод подстановкисводит определенный интеграл 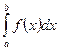с помощью подстановки 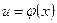к определенному интегралу относительно новой переменной и. При этом старые пределы интегрирования а и b заменяются соответственно новыми пределами интегрирования а₁ и b₁, которые находятся из исходной подстановки: ,

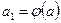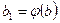
Пример 4. Решение:

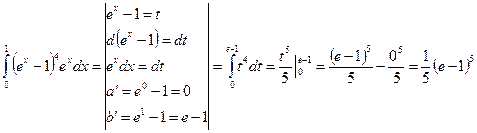
4.5 Геометрический смысл определенного интеграла

Геометрический смысл определённого интеграла: площадь фигуры, ограниченной кривой у = f (х), где f (х) 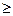0, осью ОХ и двумя прямыми х = а и х = b (рис. 1), выражается

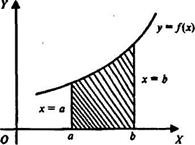
определённым интегралом: S =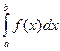

Рис1

Пример 1:определить площадь S фигуры, заключённой между ветвью кривой у = х², осью ОХ и прямыми х = 0, х = 3 (рис.2).

Решение: S=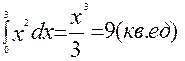

Пример 2:Найти площадь S фигуры, заключённой между осью ОХ и кривой у=х²-4х (рис.3)

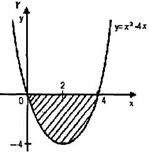
рис. 3

Решение: рассмотрим точки пересечения кривой у = х² - 4х с осью ОХ

х²-4х = 0 х(х-4) = 0 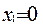или х₂ = 4.

Найдём производную функции 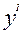= 2х - 4 и точки экстремума:

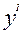= 0 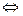2х-4 = 0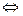^:х = 2^: у" =2>0 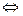х = 2 - точка min y(2) = - 4

Искомая площадь ограничена сверху OX, снизу y = х² – 4x, слева х = 0, справа

х = 4. Так как у < 0, то

S= 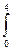(x² -4х)dх = 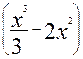= = 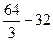= = 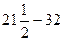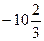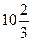(кв. ед.)

Пример 3: Найти площадь фигуры, заключённой между 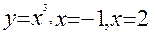и осью OX (рис.4 )

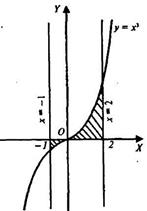
рис. 4

Найдем точки пересечения графика функции 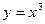с осью абсцисс .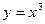

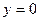
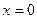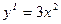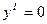
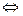
Точки экстремума: ; ; 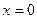; ; 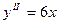; 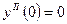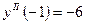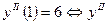меняет знак при переходе через х=0 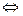т. (0;0) - точка перегиба. Значит, искомая площадь состоит из двух частей:

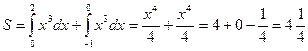(кв.ед.)

Лекция 5. Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения. Однородные дифференциальные уравнения первого порядка. Линейные однородные уравнения второго порядка с постоянными коэффициентами.

5.1 Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения.

Дифференциальным уравнением первого порядка называется равнение вида:

F(x,y,y') = 0. (1)

т.е. содержит независимую переменную х, искомую функцию у(х)и её производную у'(х).

Разрешая уравнение (1), если это возможно, относительно производной у' получим

y'=f(x,y). (2)

Иногда уравнения (1), (2) записывают в дифференциалах:

P(x,y)dx + Q(x,y)dy = O. (3)

Дифференциальное уравнение имеет, вообще говоря, бесконечное множество решений. Всякое отдельно взятое решение дифференциального уравнения называется его частным решением.
Для многих дифференциальных уравнений первого порядка общее решениеможно задать
формулой вида:

у - у(х, С), (4)

где С - произвольная постоянная такая, что при любом С функция (4) является частным решением дифференциального уравнения. С геометрической точки зрения совокупность всех решений дифференциального уравнения представляет собой семейство кривых, называемых интегральными кривыми, а каждое частное решение представляет собой отдельную интегральную кривую. Иногда не удаётся получить решения дифференциального уравнения в явной форме, т.е в виде у = у(х, С), а получают их в неявной форме, т.е. решение задаётся формулой вида:

Ф (у, х,С)=0 (5)

Выражение типа Ф (х, у, С) = 0 в этом случае называют интегралом (частным, общим)дифференциального уравнения.

Задача Коши.

В случае дифференциального уравнения первого порядка задача Коши формулируется следующим образом: найти решение у = у(х) уравнения у' =f(x, у), удовлетворяющее начальному условию у 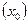= у, где 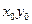- заданные числа. Задача Коши кратко записывается так:

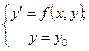при х=х0. (6)

Геометрически решение, удовлетворяющее начальному условию у (х 0)=у 0, представляет интегральную кривую, проходящую через данную точку (х_о;у_о).

Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
Дифференциальное уравнение (2) называется уравнением с разделяющимися переменными, если имеет следующий вид:

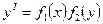(7)

В предположении, что f2 (y) 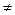0, уравнение с разделяющимися переменными (7) можно переписать в виде (разделить переменные):

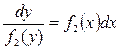(8)

Уравнение вида (8) называется уравнением с разделёнными переменными.

Теорема 1. Если существуют интегралы 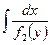и 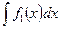, то общий интеграл уравнения с разделёнными переменными (8) задаётся уравнением

F2 (у) = F1(x) + C, (9)

где F2 (у) и Fx (х) - некоторые первообразные соответственно функций.

При решении дифференциальных уравнений с разделяющимися переменными можно руководствоваться следующим алгоритмом:

1) разделить переменные (с учётом условий, когда это можно делать);

2) проинтегрировать почленно полученное уравнение с разделёнными переменными;

3) найти его общий интеграл;

4) выяснить, имеет ли уравнение (5) решения, не получающиеся из общего интеграла;

5) найти частный интеграл (или решение), удовлетворяющий начальным условиям (в случае задачи Коши).

Пример1.Найти частное решение уравнения: 2уу' = 1 - Зх²; у0 = 3 при х0 = 0

Решение: это уравнение с разделяющимися переменными. Представим его в дифференциалах.

Учитывая, что 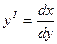получим 2у— = 1-3х .

Разделим переменные:

2ydy = (1 - Зх² )dx. Интегрируя обе части последнего равенства, найдём

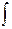2ydy = 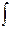(1 - Зх² )dx, т.е. у2=х-х³+С. Подставив начальные значения х0 =1, уо=3,

найдём С: 9=1-1+С, т.е. С=9. Следовательно, искомый частный интеграл будет у²=х-х³+9, или х³+у²-х-9 = 0

<5 6 789 10 11 >

Дата добавления: 2020-05-20; просмотров: 491;