Модуль 10. Определенный интеграл
10.1. Основные свойства и методы вычисления
Пусть функция f(x) задана в некотором отрезке 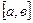 . Разобьем отрезок на n частей точками а< х0< х1<…< хn< в. Обозначим
. Разобьем отрезок на n частей точками а< х0< х1<…< хn< в. Обозначим 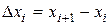 через
через 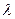 . Выберем в каждом промежутке
. Выберем в каждом промежутке 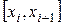 произвольную точку
произвольную точку 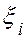 и составим сумму
и составим сумму
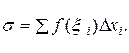 (25)
(25)
Если существует конечный предел интегральной суммы (25) при 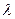
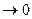 , то его называют определенным интегралом функции f(x) в промежутке от адо ви обозначается
, то его называют определенным интегралом функции f(x) в промежутке от адо ви обозначается 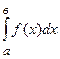 .
.
Основные свойства определенного интеграла:
1. При перестановке пределов изменяется знак интеграла:
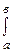 f(x)dx = -
f(x)dx = - 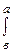 f(x)dx .
f(x)dx .
2. Интеграл с одинаковыми пределами равен нулю: 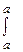 f(x)dx = 0.
f(x)dx = 0.
3. Отрезок интегрирования можно разбить на части:
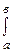 f(x)dx =
f(x)dx = 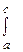 f(x)dx +
f(x)dx + 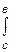 f(x)dx .
f(x)dx .
4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых:
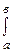 [ f
[ f 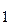 (х) + f2 (х) – f3 (х)] dx =
(х) + f2 (х) – f3 (х)] dx = 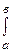 f1 (x)dx +
f1 (x)dx + 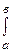 f2 (x)dx +
f2 (x)dx + 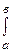 f3 (x)dx .
f3 (x)dx .
5. Постоянный множитель можно выносить за знак интеграла:
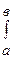 сf(x)dx = с
сf(x)dx = с 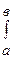 f(x)dx.
f(x)dx.
6. Если функция f(x), интегрируемая на отрезке 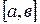 , и f(x) ³ 0 для всех х Î
, и f(x) ³ 0 для всех х Î 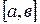 , то
, то 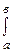 f(x)dx ³ 0.
f(x)dx ³ 0.
7. Если функции f(x), j(х) интегрируемы на отрезке 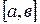 и
и
f(x) £ j(х) для всех х Î 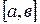 , то
, то 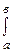 f(x)dx £
f(x)dx £ 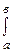 j(х)dx.
j(х)dx.
Для вычисления определенного интеграла, когда можно найти соответствующий неопределённый интеграл, служит формула Ньютона – Лейбница:
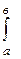 f(x)dx = F(x )
f(x)dx = F(x ) 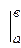 = F(b) - F(a) (26)
= F(b) - F(a) (26)
Пример 67. Вычислить интеграл 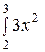 dx.
dx.
Решение. Применяя формулу (26) и свойства определенного интеграла, получим
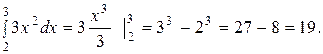
Правило интегрирования по частям в определенном интеграле:
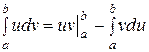 ,
,
где u и v - функции независимой переменной.
Пример 68. Вычислить интеграл 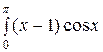 .
.
Решение:
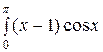 =
= 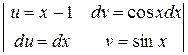 = (х -1)cos
= (х -1)cos 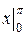 -
- 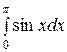 = (p - -1)cosp +1+ cos
= (p - -1)cosp +1+ cos 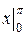 = 1 - p + 1 -1 - 1 = - p.
= 1 - p + 1 -1 - 1 = - p.
Правило замены переменной в определенном интеграле:
Если в интервале 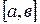 функции х = j(t), j¢(t) и f (j(t)) -непрерывны и j(а) = a, j(в) = b, то
функции х = j(t), j¢(t) и f (j(t)) -непрерывны и j(а) = a, j(в) = b, то
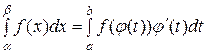 .
.
Пример 69.Вычислить интеграл 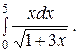
Решение:
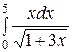 =
= 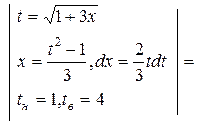
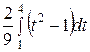 =
= 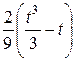
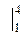 =
=
= 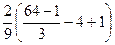 = 4.
= 4.
Дата добавления: 2020-07-18; просмотров: 617;











