Интеграл от рациональной дроби.
В пункте г) вашей контрольной работы предлагается взять интеграл от рациональной дроби.
Пример.
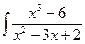
Под знаком интеграла стоит рациональная дробь.
1. Так как подинтегральная рациональная дробь неправильная (степень многочлена в числителе выше степени многочлена в знаменателе),то выделим целую часть, разделив числитель на знаменатель “углом” (аналогично тому, как в задачах 41-50):
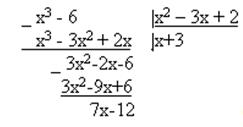
Итак, подынтегральную функцию можно записать в виде:
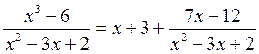
Тогда данный интеграл (обозначим его J), можно представить как сумму интегралов:
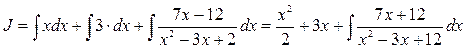
2. Чтобы взять полученный новый интеграл от правильной рациональной дроби (обозначим его J1, разложим знаменатель подынтегральной функции на множители.
Для этого найдем корни квадратного трехчлена, стоящего в знаменателе: x2-3x+12=0.
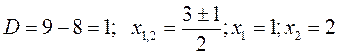
Тогда
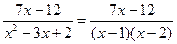
3. Представим полученную правильную дробь в виде суммы элементарных дробей:
4. 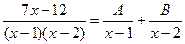 (*)
(*)
Здесь А и В - числа, которые нужно найти. Сделаем приведение к общему знаменателю в правой части:
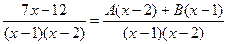
Так как дроби тождественно равны и равны их знаменатели, то должны быть равны и их числители:
7x-12=A(x-2)+B(x-1);
7x-12=Ax-2A+Bx-B;
7x-12=(A+B)x+(-2A-B).
Это тождество выполняется тогда и только тогда, когда слева и справа равны коэффициенты при одинаковых степенях х:
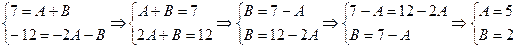
Получена система двух уравнений с двумя неизвестнымиА и В, решив которую, найдем А=5; В=2.
Подставим найденные числа в равенство (*):
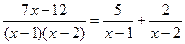
4. Вернемся к интегралу J1:
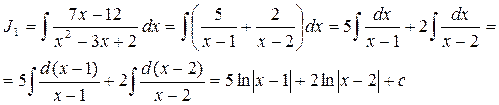
5. Окончательно искомый интеграл равен:
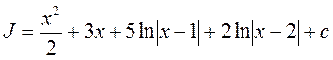
Дата добавления: 2020-05-20; просмотров: 780;











