Функции нескольких переменных. Частные производные

<2 3 456 7 8 >

Пусть задана функция z=f(x,y). Так как x и y - независимы переменные, то одна из них может изменяться, а другая сохранять свое значение.

О: Если существует предел

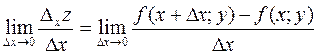то он называется частной производной функции z=f(x,y) в точке М(х,у) по переменной х и обозначается одним их символов:

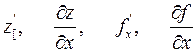Частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции f(x,y) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х и у считается постоянной величиной ).

Формула полного дифференциала функции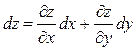

ПРИМЕР: Найти полный дифференциал функции двух переменных

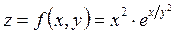
Решение.

Полный дифференциал функции двух переменных находим по формуле:

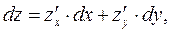
где z^/_x ; z^/_y – частные производные данной функции z.

Частные производные берем по обычным формулам дифференцирования для функции одной переменной, причем z^/_x находим, считая “y” постоянной величиной; аналогично при отыскании z^/_y считаем “x” постоянным:

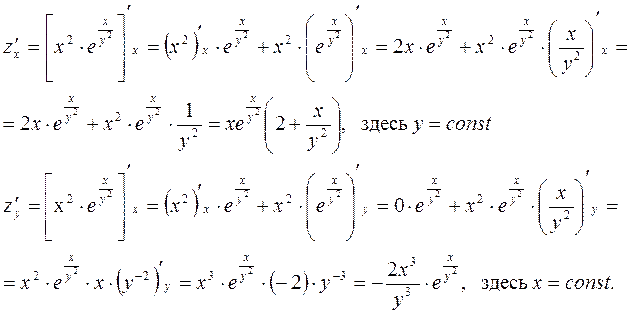
Отсюда полный дифференциал функции :

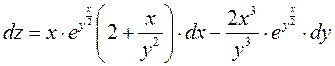
Лекция 4. Неопределенный интеграл. Методы интегрирования. Определенный интеграл. Вычисление определенного интеграла. Геометрический смысл определенного интеграла.

4.1 Неопределенный интеграл.

Определение 1. Функция F(x) называется первообразной для функции f(x) в промежутке 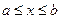, если в любой точке этого промежутка ее производная равна f(x):

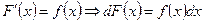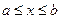, . (1)

Определение 2. Совокупность всех первообразных функций F(x) + с для функции f(x) на некотором промежутке называется неопределённым интеграломи обозначается

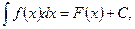(2)

где f(x)dx называется подынтегральным выражением, х - переменной интегрирования, а С -произвольной постоянной интегрирования. Процесс нахождения первообразной функции называется интегрированием. Например 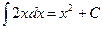, т.к.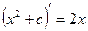

<2 3 456 7 8 >

Дата добавления: 2020-05-20; просмотров: 570;