Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона
Пусть функция y(x), задана таблично в равноотстоящих узлах xi на отрезке [a,b]:
| x | x0 | x1 | x2 | … | xn |
| f(x) | y0 | y1 | y2 | … | yn |
Для нахождения на [a,b] производных 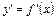 ,
, 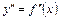 и т.д., функцию y приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов
и т.д., функцию y приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов 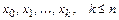 :
:
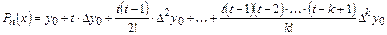
где 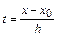 и
и 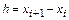 .
.
Производя перемножение биномов, получим:
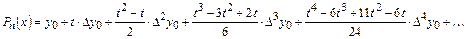
Будем дифференцировать данный многочлен как сложную функцию: 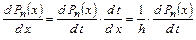 . Получим:
. Получим:
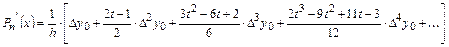
| (1) |
Так как 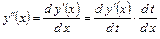 , формула вычисления второй производной будет выглядеть следующим образом:
, формула вычисления второй производной будет выглядеть следующим образом:
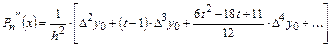
| (2) |
Таким же способом можно вычислить производные любого порядка.
Чтобы уменьшить погрешность вычисления, при нахождении производных в фиксированной точке х в качестве х0 следует выбирать ближайшее табличное значение аргумента (уменьшить таблицу).
Иногда требуется находить производные функции в основных табличных точках xi. В этом случае формулы численного дифференцирования упрощаются. Так как каждое табличное значение можно считать за начальное, то положим x=x0, следовательно, t=0.
Получим:
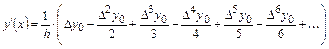
| (3) | |
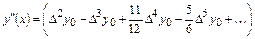
| (4) |
Погрешность приближенного вычисления первой производной в нулевой точке будет равна
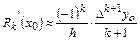
Пример 1. Приняв шаг h = 0,05, построить на отрезке [3,5; 3,6] интерполяционный полином Ньютона для функции у = ех, заданной таблицей
| х | 3,50 | 3,55 | 3,60 | 3,65 | 3,70 |
| у | 33,115 | 34,813 | 36,598 | 38,475 | 40,447 |
Составляем таблицу разностей (Таблица 3).
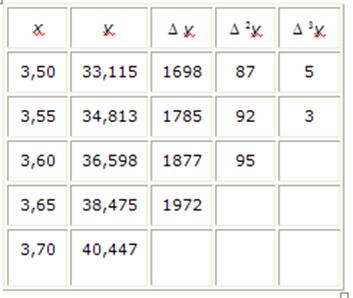
Заметим, что в столбцах разностей, следуя обычной практике, мы не указываем десятичные разряды (которые ясны из столбца значений функции). Так как разности третьего порядка практически постоянны, то в формуле (15) полагаем n = 3. Приняв x0 = 3,50, y0= 33,115, будем иметь:
P3 (x) = 33,115+ 1,698 t + 0,087 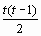 + 0,005
+ 0,005 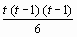
или
P3 (x) = 33,115+ 1,698 t + 0,0435 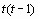 + 0,00083
+ 0,00083 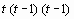 ,
,
где
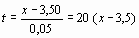 .
.
На практике часто необходимо для функции, заданной таблично, подобрать аналитическую формулу, представляющую с некоторой точностью данные табличные значения функции. Такая формула называется эмпирической, причем задача построения ее неоднозначна.
При построении эмпирической формулы следует учитывать общие свойства функции. Если из таблицы разностей будет обнаружено, чтоn-е разности функции для равностоящих значений аргумента постоянны, то в качестве эмпирической формулы можно взять соответствующую первую интерполяционную формулу.
Пример 2. Построить эмпирическую формулу для функции у, заданной таблично
| х | ||||||
| у | 5,2 | 8,0 | 10,4 | 12,4 | 14,0 | 15,2 |
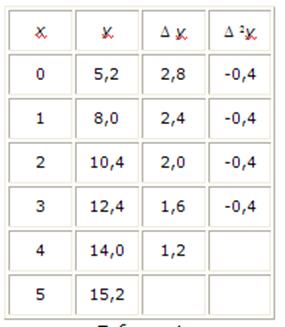
Таблица 4
Составляя таблицу разностей (Таблица 4), убеждаемся, что вторая разность постоянна.
Используя интерполяционную формулу Ньютона в форме (14) и учитывая, что h = 1, будем иметь:
у = 5,2 + 2,8 х - 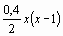
или
у = 5,2 + 3 х - 0,2 х2.
Дата добавления: 2020-05-20; просмотров: 1196;











