Интегрирование способом подстановки (замена переменной)
Сущность интегрирования методом подстановки заключается в преобразовании интеграла 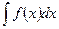 в интеграл
в интеграл 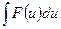 , который легко вычисляется по какой-либо из основных формул интегрирования. Для нахождения
, который легко вычисляется по какой-либо из основных формул интегрирования. Для нахождения 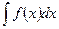 заменяем переменную х новой переменной и с помощью подстановки.
заменяем переменную х новой переменной и с помощью подстановки. 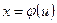 .Дифференцируя это равенство, получаем
.Дифференцируя это равенство, получаем 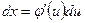 . Подставляя в подынтегральное выражение вместо х и dx их значения, выраженные через
. Подставляя в подынтегральное выражение вместо х и dx их значения, выраженные через 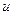
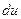 , имеем
, имеем
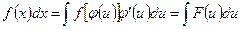 (3)
(3)
После того, как интеграл относительно новой переменной и будет найден, с помощью подстановки 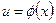 он приводится к переменной х.
он приводится к переменной х.
Примеры:
l) 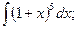 2)
2) 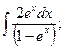
Решение:
1) положим 1 + х = z. Продифференцируем это неравенство: 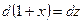 или dx = dz.
или dx = dz.
Заменим в интеграле: 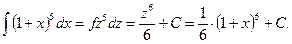
2)Сделав замену: 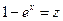 , получим
, получим 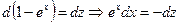 . Тогда
. Тогда
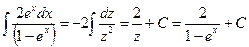
4. 4 Интегрирование “по частям”
Интеграл из пункта в) вашей контрольной работы берется методом интегрирования “по частям”. Этим методом интегрируются некоторые произведения, например произведения степенной функции на логарифмическую или на показательную, или на тригонометрическую, или на обратные тригонометрические функции и др.
Интегрирование “по частям” производится по формуле
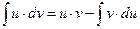
Чтобы воспользоваться этой формулой, следует один множитель в подынтегральном выражении обозначить за “u”, а оставшийся множитель вместе с dx принять за “dv”.
Для того, чтобы интеграл в правой части был проще данного интеграла, надо правильно выбрать “u” и “dv”.
В интегралах, берущихся по частям, обычно логарифмическую и обратные тригонометрические функции принимают за “u”. Если подынтегральная функция содержит произведение степенной функции на показательную или тригонометрическую, то за “u” принимается степенная функция.
Пример.
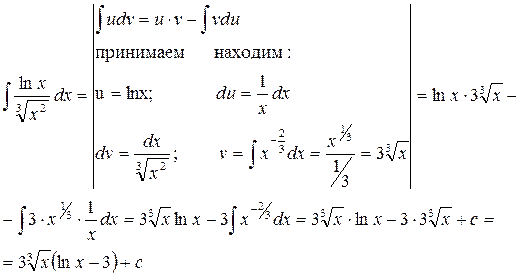

Пример.
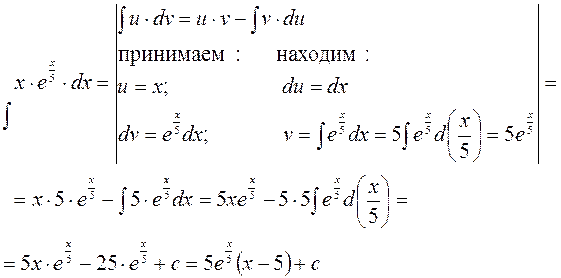
Дата добавления: 2020-05-20; просмотров: 680;











