Однородные дифференциальные уравнения первого порядка.
Уравнение вида 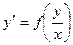 (1) называется однородным уравнением.
(1) называется однородным уравнением.
Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой y=ux, где u – новая искомая функция. Дифференцируя равенство y=ux, получим 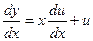 (2) .
(2) .
Подставив выражения у и 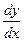 в уравнение (1), имеем
в уравнение (1), имеем
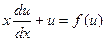
откуда
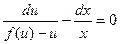 (3)
(3)
Это уравнение с разделяющимися переменными. Найдя общее решение уравнения (3), получаем общее решение данного уравнения (1), заменив u на у/х.
Пример: Найти I) общее решение уравнения 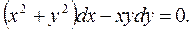
II) частное решение данного уравнения, удовлетворяющий заданным начальным условиям: у(2)=0
Решение:
I) Разрешим уравнение относительно производной 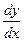 :
: 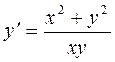 .
.
Поделив числитель и знаменатель правой части уравнения на х2, получим
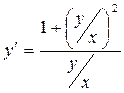 (*)
(*)
Замены: u=y/x и 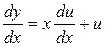 в уравнение (*).
в уравнение (*).
Уравнение (*) преобразуется в уравнение с разделяющимися переменными:
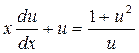 Û
Û 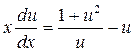 Û
Û 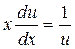 откуда
откуда 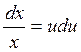
Интегрируя это уравнение, получим 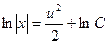 Û
Û 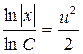 т.е. х=С
т.е. х=С 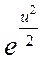
Заменяя в последнем равенстве u на y/x, окончательно получаем общее решение данного уравнения х=С 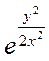
II)Используя начальные условия у(2)=0, подставляем в общее решение данного уравнения х=С 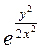 , заданные значения переменных х=2, у=0 – тем самым определяем значение произвольной постоянной С: 2=С
, заданные значения переменных х=2, у=0 – тем самым определяем значение произвольной постоянной С: 2=С 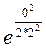 Û С= 2.
Û С= 2.
Итак, искомое частное решение х=2 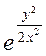
Дата добавления: 2020-05-20; просмотров: 793;











