Определенный интеграл и его свойства
Задача о вычислении площади криволинейной трапеции
Пусть функция 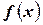 непрерывна на отрезке
непрерывна на отрезке 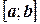 и
и 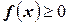 . Рассмотрим фигуру, ограниченную графиком
. Рассмотрим фигуру, ограниченную графиком 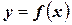 , отрезком
, отрезком 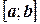 оси абсцисс и линиями
оси абсцисс и линиями 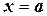 и
и 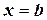 . Такую фигуру назовём криволинейной трапецией (рис. 4.3).
. Такую фигуру назовём криволинейной трапецией (рис. 4.3).
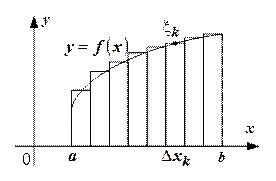
Рис. 4.3.
Вычислим площадь этой фигуры. Для этого точками 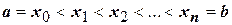 разобьем отрезок
разобьем отрезок 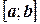 на частичные отрезки
на частичные отрезки 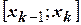 и обозначим
и обозначим 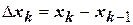 . Для каждого отрезка
. Для каждого отрезка 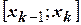 выберем произвольную точку
выберем произвольную точку 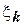 и построим прямоугольник с основанием
и построим прямоугольник с основанием 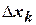 и высотой
и высотой 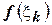 как показано на рисунке. Площадь такого прямоугольника будет равна
как показано на рисунке. Площадь такого прямоугольника будет равна 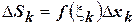 . А площадь всей фигуры соответственно
. А площадь всей фигуры соответственно 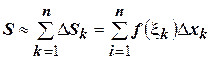 . Это равенство будет тем точнее, чем на большее количество отрезков
. Это равенство будет тем точнее, чем на большее количество отрезков 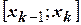 разбит отрезок
разбит отрезок  , то есть
, то есть 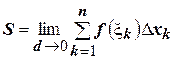 (где
(где 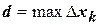 ).
).
К необходимости вычисления таких пределов приводит целый ряд других задач, таких как вычисление длины линии, вычисление объема тела, вычисление площади поверхности вращения, вычисление работы и др.
Определенный интеграл и его свойства
Пусть на отрезке 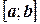 задана непрерывная функция
задана непрерывная функция 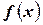 . Разобьем точками
. Разобьем точками 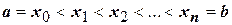 отрезок
отрезок 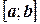 на частичные отрезки
на частичные отрезки 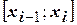 и примем
и примем 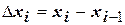 . На каждом частичном отрезке выберем точку
. На каждом частичном отрезке выберем точку 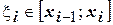 . Сумму
. Сумму
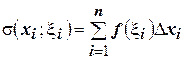 (4.21)
(4.21)
называют интегральной суммой, соответствующей данному способу разбиения отрезка 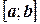 на части и данному способу выбора точек
на части и данному способу выбора точек 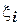 на каждом из частичных отрезков.
на каждом из частичных отрезков.
Если существует предел суммы (4.21), не зависящий от способа разбиения отрезка 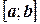 и способа выбора точек
и способа выбора точек 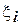 , то его называют определенным интегралом от функции
, то его называют определенным интегралом от функции 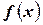 по отрезку
по отрезку 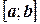 и записывают
и записывают
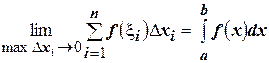 . (4.22)
. (4.22)
Справедливо утверждение: если функция 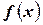 непрерывна на
непрерывна на 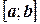 , то определенный интеграл
, то определенный интеграл 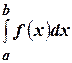 всегда существует.
всегда существует.
Замечание:
1). Вообще – то интеграл (4.22) существует и при менее жестких требованиях, накладываемых на функцию 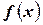 . Однако в нашем курсе будем предполагать, что функция
. Однако в нашем курсе будем предполагать, что функция 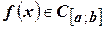 .
.
2). В соответствии с (4.22) площадь криволинейной трапеции (см. п. 4.14) вычисляется по формуле
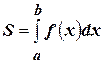 (4.23)
(4.23)
Отметим основные свойства определённых интегралов:
1) 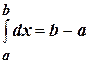
Доказательство:
Так как 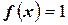 , то интегральная сумма для интеграла
, то интегральная сумма для интеграла 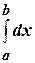 примет вид
примет вид 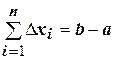 . Переходя к пределу, получим
. Переходя к пределу, получим
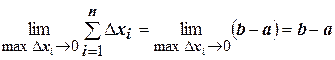 . ☻
. ☻
2) 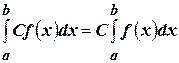 , где
, где 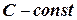 .
.
Доказательство:
Составим интегральную сумму и перейдем к пределу: 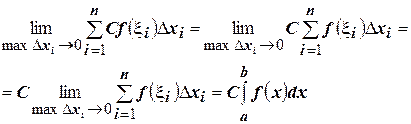 ☻
☻
3) Если существуют 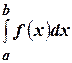 и
и 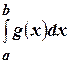 , то существует и
, то существует и 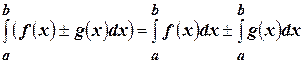 .
.
Доказательство:
Составим интегральную сумму для интеграла 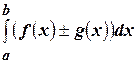 и перейдем в ней к пределу. Получим
и перейдем в ней к пределу. Получим
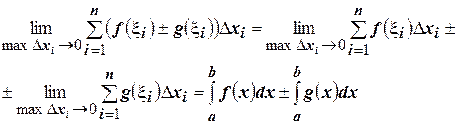 ☻
☻
4) По соглашению 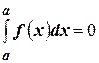
5) По соглашению 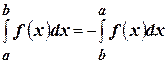
6) Если 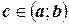 , то
, то 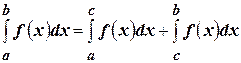 .
.
Доказательство:
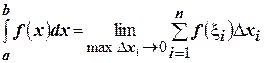
Поскольку этот предел не зависит от способа разбиения отрезка 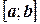 , то возьмем такой способ разбиения, чтобы точка
, то возьмем такой способ разбиения, чтобы точка 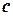 была одной из точек разбиения отрезка
была одной из точек разбиения отрезка 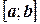 . Тогда:
. Тогда:
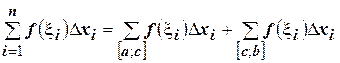
И переходя к пределу, получим:
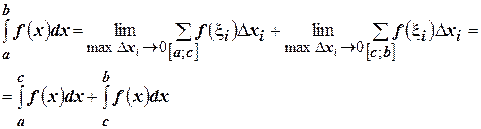
Это свойство остаётся в силе и при любом расположении точек  .
.
Например, если 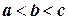 и функция
и функция 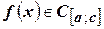 , то
, то
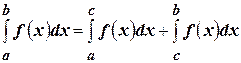 . ☻
. ☻
7) Если 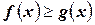 , то
, то 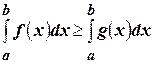 , причем равенство будет только в том случае, если
, причем равенство будет только в том случае, если 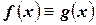 .
.
Доказательство:
Имеем 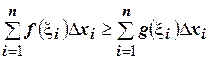 , т.к. слагаемые в сумме, стоящей в левой части неравенства, не меньше соответствующих слагаемых правой суммы. Переходя к пределу в неравенстве, получим требуемый результат. ☻
, т.к. слагаемые в сумме, стоящей в левой части неравенства, не меньше соответствующих слагаемых правой суммы. Переходя к пределу в неравенстве, получим требуемый результат. ☻
8) Если 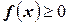 , то
, то 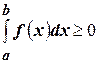 ,
,
а если 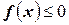 , то
, то 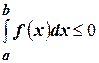 .
.
Это свойство определённых интегралов является следствием предыдущего свойства.
9) 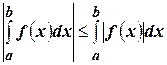
Доказательство:
Проинтегрируем неравенство 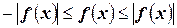 и получим
и получим
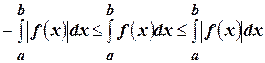 ,
,
что как раз и означает, что
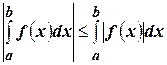 .☻
.☻
Дата добавления: 2020-10-25; просмотров: 486;











