Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Дифференциальные уравнения второго порядкав общем случае записывается в виде:
F(x,y,y',y") = 0. (1)
или, если это возможно, в разрешённом относительно у" виде
y" = f(x,y,y 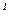 ). (2)
). (2)
Определение 1. Говорят, что формула у = f(х,С1,С2) представляет общее решениедифференциального уравнения второго порядка (1) или (2), если для любых значений С 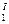 и С'2 постоянных С
и С'2 постоянных С 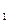 , и С
, и С 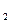 функция f(х,С,',С'2)является решением данного уравнения, и любое его частное решениеможет быть получено из формулы у=f(х,Сх,С2) при некоторых значениях С
функция f(х,С,',С'2)является решением данного уравнения, и любое его частное решениеможет быть получено из формулы у=f(х,Сх,С2) при некоторых значениях С 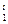 и С'2.
и С'2.
Для дифференциальных уравнений второго порядка задача Кошиформулируется следующим образом: найти решение у= у(х) уравнения у" = f(x,y,y'), удовлетворяющее начальным условиям у(х0) = у0, у'(х0) = у'о или, в другой записи,
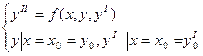 (3)
(3)
где х0,у0,у'о - заданные числа. Геометрически общее решение уравнения (1) или (2) представляет собой семейство интегральных кривых, а решение, удовлетворяющее начальным условиям у(х0) = у0, у'(х0) = у'о, представляет интегральную кривую, проходящую через данную точку (дг0; >>0) в данном направлении - угловой коэффициент касательной к интегральной кривой (графику решения у = у(х)), проведённой в точке (х0; у0) равен данному числу у'о. Простейшее уравнение второго порядка имеет вид
y 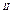 = f(x) (4)
= f(x) (4)
Уравнения этого вида решаются двукратным интегрированием:
полагаем у' = р(х), тогда у" = р' и уравнение (4) принимает вид p' = f(x), или dp=f(x) dx.
Отсюда р = 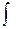 f(x)dx = F(x) + С,, где F(x) - одна из первообразных для функции f(x).
f(x)dx = F(x) + С,, где F(x) - одна из первообразных для функции f(x).
Так как р =у', то у' = F(x) + C или dy = (F(x) + Сх )dx. Отсюда, интегрируя ещё раз, находим, как нетрудно проверить, общее решение уравнения (4) (в области, где существуют рассматриваемые интегралы):
у = 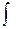 F{x)dx + С,х + С2
F{x)dx + С,х + С2
Пример 1.Найти общее решение уравнения у" = cos2x.
Решение: положим у' = р(х); тогда у" = р', и, следовательно, р' = cos 2x или dp = cos 2xdx.
Интегрируя это уравнение, находим: р = — sin 2x + С,, или у' = -sin2х + С,
т..е. dy = -sin2xdx + Cdx.
Интегрируя второй раз, находим общее решение: 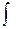 dy =
dy = 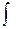 — sin 2xdx + С,
— sin 2xdx + С, 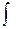 dx, т.е. y = —cos 2x + С, x + С2.
dx, т.е. y = —cos 2x + С, x + С2.
Уравнение вида 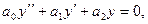 (5)
(5)
где 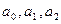 - действительные числа
- действительные числа 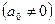 , называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Чтобы решить уравнение (1), нужно решить характеристическое уравнение:
, называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Чтобы решить уравнение (1), нужно решить характеристическое уравнение:
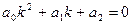 (6)
(6)
При решении характеристического уравнения (6) возможны три случая, в зависимости от которых строится общее решение данного дифференциального уравнения (5)
| Корни уравнения (2) | Частные решения уравнения (1) | Общее решение уравнения (1) |
Действительные и различные:
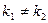
| 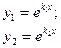
| 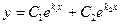
|
Равные: 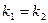
| 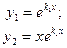
| 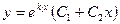
|
Комплексно сопряженные 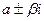
| 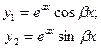
| 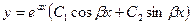
|
Пример 2. Найти общее решение уравнений:
а) 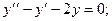
б) 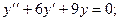
в) 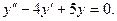
Решение:
а) Составим характеристическое уравнение: 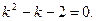
Его корни 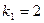 и
и 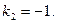 Значит, общее решение уравнения имеет вид
Значит, общее решение уравнения имеет вид 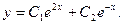
б) Составим характеристическое уравнение: 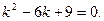
Его корни 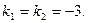 Тогда общее решение имеет вид
Тогда общее решение имеет вид 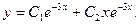
в) Составим характеристическое уравнение: 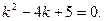
Решая его, получим D = -4 и комплексно сопряженные корни 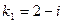 и
и 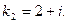 Тогда его общим решением будет
Тогда его общим решением будет 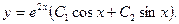
Лекция 6. Методы интегрирования. Метод прямоугольников. Метод трапеций. Метод Симпсона. Абсолютная погрешность при численном интегрировании
1. Метод прямоугольников.
Предположим, что перед нами 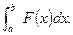 Перепробовав все известные способы, нам не удалось его вычислить.
Перепробовав все известные способы, нам не удалось его вычислить.
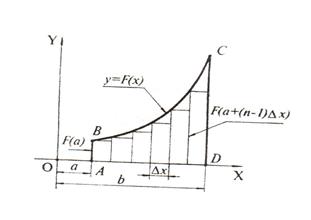
Теперь попробуем построить в системе XOY фигуру, которой данный интеграл соответствует, хотя бы ориентировочно.
Вычислить 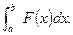 - это значит найти площадь фигуры ABCD.
- это значит найти площадь фигуры ABCD.
Разобьем ее как показано на чертеже. Очевидно, что площадь АВСД=Q1+Q2, где Q1- площадь всех прямоугольников, а Q2- площадь всех криволинейных треугольников.
Если число делений высоты фигуры AD велико, то Q2 значительно меньше Q1(Q2<<Q1), и тогда можно принять, что S ABCD=Q1, но 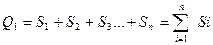 , где Si - площадь одного прямоугольника.
, где Si - площадь одного прямоугольника.
По чертежу находим:
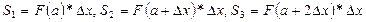 и т.д.
и т.д.
Таким образом получаем:
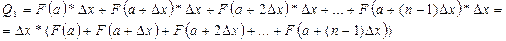
Итак, данный интеграл 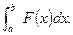 свелся к нахождению площади Q1
свелся к нахождению площади Q1
ВЫВОД:
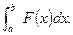
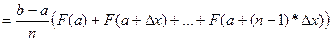
Очевидно, что чем больше число делений n, следовательно число слагаемых в скобке, тем точнее результат получим при вычислении того или иного определенного интеграла.
Способ трапеций
Пусть мы имеем интеграл 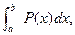 который так же известными способами вычислять не удалось.
который так же известными способами вычислять не удалось.
Построим в системе координат XOY фигуру, которой данный интеграл соответствует, хотя бы ориентировочно.
Вычислить 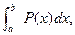 - это значит найти площадь фигуры ABCD. Разобьем ее как показано на чертеже. Очевидно, что SАВСД =Q1+Q2, где Q1- площадь всех трапеций, а Q2- площадь всех криволинейных треугольников.
- это значит найти площадь фигуры ABCD. Разобьем ее как показано на чертеже. Очевидно, что SАВСД =Q1+Q2, где Q1- площадь всех трапеций, а Q2- площадь всех криволинейных треугольников.
Если делений основания AD фигуры велико, то тогда можно принять, что SАВСД ≈ Q1, но 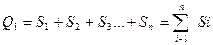 , где Si- площадь i-той трапеции.
, где Si- площадь i-той трапеции.
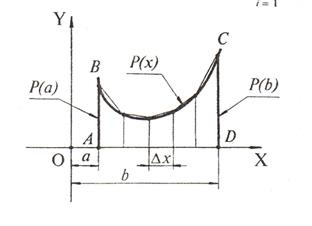
Из чертежа находим:
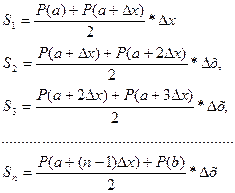 Здесь
Здесь 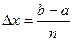
Таким образом, получаем:
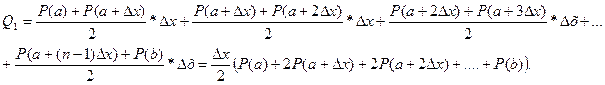
Окончательно имеем
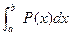 =
= 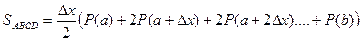
Существует еще более точный способ вычисления определенных интегралов- способ парабол ( метод Симпсона- по имени немецкого математика, предложившего его), но в данной практической он не рассматривается.
Пример 1Вычислить 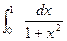 по методу прямоугольника и трапеции, сравнить результаты. Число делений n принять равным 5.
по методу прямоугольника и трапеции, сравнить результаты. Число делений n принять равным 5.
Решение
1) по методу прямоугольников имеем
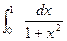 =
= 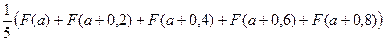
здесь 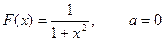 , тогда
, тогда

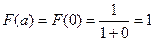
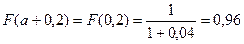
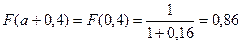
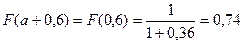
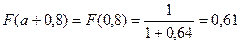
Получаем 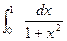 по методу прямоугольников примерно равен 0,83
по методу прямоугольников примерно равен 0,83
2) По методу трапеций
Получаем 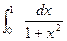 =
= 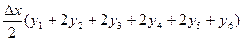
Здесь 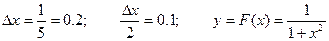
y1 = f(0) = 1
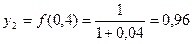
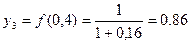
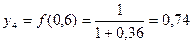
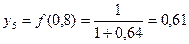
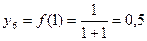
Окончательно 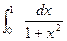 по способу трапеций примерно равен 0,791.
по способу трапеций примерно равен 0,791.
Очевидно что метод трапеций более точный способ, так как значение данного интеграла до 3-го знака после запятой будет
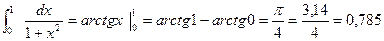
Пример 2.Вычислить приближённое значение определённого интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления производить с округлением третьего десятичного знака.
Решение.Формула Симпсона или формула парабол имеет вид:
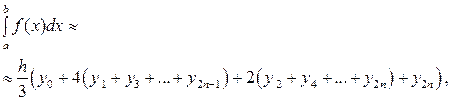 (1)
(1)
где 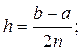
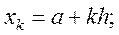
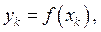
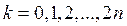 .
.
Рассмотрим 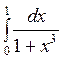 при
при 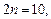 тогда
тогда 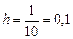 .
.
Составим таблицу значений подынтегральной функции, необходимых для вычисления данного интеграла.
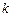
| 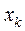
| 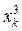
| 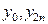
| уk (k - нечетное) | уk (k - четное) |
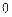
| 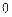
| 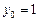
| |||
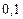
| 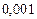
| 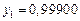
| |||
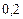
| 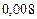
| 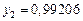
| |||
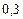
| 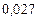
| 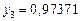
| |||
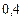
| 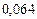
| 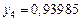
| |||
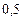
| 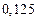
| 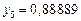
| |||
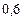
| 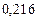
| 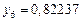
| |||
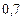
| 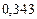
| 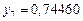
| |||
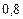
| 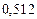
| 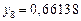
| |||
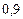
| 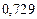
| 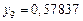
| |||
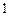
| 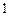
| 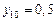
| |||
| ∑ | 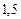
| 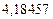
| 
|
В последней строке таблицы находятся суммы чисел соответствующих столбцов.
Так как
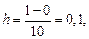
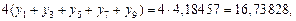
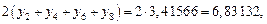
по формуле (1) находим
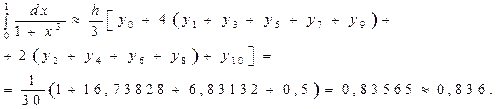
3. Точностные оценки
Оценка погрешности усечения рассматриваемых формул численного интегрирования по выражениям для остаточных членов часто оказывается малоэффективной из-за трудностей оценки производных высокого порядка подынтегральных функций. На практике для достижения требуемой точности прибегают к методу последовательного удвоения числа шагов. Задают значения допустимой погрешности и начальное число n0 шагов. Вычисляют величину интеграла по выбранной квадратурной формуле при числе интервалов n0 и 2n0 (соответственно In и I2n). По правилу Рунге оценивается погрешность приближенного значения интеграла
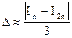 - для формулы трапеций;
- для формулы трапеций;
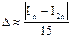 - для формулы Симпсона.
- для формулы Симпсона.
Если D³e, то количество интервалов разбиения увеличивают вдвое, т.е. значения интеграла вычисляются для последовательных значений n=n0,2n0,4n0,...Вычисления заканчиваются при выполнении условия D<e.
Оценка погрешности усечения при интегрировании функций, заданных таблично:
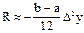 - для формулы трапеций
- для формулы трапеций
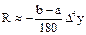 - для формулы Симпсона.
- для формулы Симпсона.
D2y, D4y, - средние арифметические значения конечных разностей соответствующего порядка. Данные оценки применяются для функций, которые достаточно хорошо интерполируются многочленом соответствующей степени.
Ошибки округления носят случайный характер, но с увеличением числа интервалов разбиения возрастают в среднем пропорционально 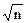 . Вследствие этого при увеличении n общая погрешность уменьшается за счет уменьшения ошибки усечения лишь до некоторого значения n. Затем погрешности округления преобладают, и общая погрешность увеличивается.
. Вследствие этого при увеличении n общая погрешность уменьшается за счет уменьшения ошибки усечения лишь до некоторого значения n. Затем погрешности округления преобладают, и общая погрешность увеличивается.
Лекция 7. Понятие о численном решении дифференциальных уравнений. Формулы приближенного дифференцирования, основанные на интерполяционных формулах Ньютона. Погрешности в определении производной. Построение интегральной кривой. Метод Эйлера
Постановка задачи
При решении практических задач часто нужно найти производные указанных порядков от функции 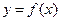 , заданной таблично, либо, в силу сложности аналитического выражения функции f(x) непосредственное ее дифференцирование затруднено. В этих случаях обычно прибегают к приближенному дифференцированию.
, заданной таблично, либо, в силу сложности аналитического выражения функции f(x) непосредственное ее дифференцирование затруднено. В этих случаях обычно прибегают к приближенному дифференцированию.
Для вывода формул приближенного дифференцирования исходную функцию f(x) заменяют на интересующем отрезке [a, b] интерполирующей функцией P(x), а затем полагают, что 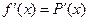 , при
, при 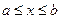 .
.
Аналогично поступают при нахождении производных высших порядков.
Если для интерполирующей функции P(x) известна погрешность 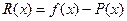 , то погрешность производной
, то погрешность производной 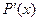 выражается формулой
выражается формулой 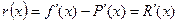 , т.е.:
, т.е.:
● Погрешность производной интерполирующей функции равна производной от погрешности этой функции.
 То же самое справедливо и для производных высших порядков.
То же самое справедливо и для производных высших порядков.
Следует отметить, что приближенное дифференцирование представляют собой операцию менее точную, чем интерполирование: близость друг к другу двух кривых 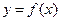 и
и 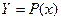 на отрезке [a, b] еще не гарантирует близости на этом отрезке их производных
на отрезке [a, b] еще не гарантирует близости на этом отрезке их производных 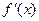 и
и 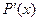 , т.е. малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента.
, т.е. малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента.
Как видно из рисунка, касательные, проведенные к графикам функций 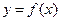 и
и 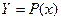 в точке xi, имеют разный угол наклона (тангенс угла наклона касательной равен производной функции в данной точке).
в точке xi, имеют разный угол наклона (тангенс угла наклона касательной равен производной функции в данной точке).
Дата добавления: 2020-05-20; просмотров: 826;











