Как вычислить определенный интеграл по формуле Симпсона?

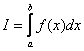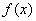И снова, начнём с общей формулы. Рассмотрим определенный интеграл , где – функция, непрерывная на отрезке 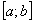. Проведём разбиение отрезка 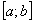на чётное количество равных отрезков. Чётное количество отрезков обозначают через .

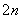На практике отрезков может быть:
два: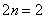
четыре: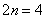
восемь: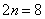
десять: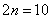
двадцать: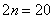
Внимание!Число 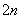понимается как ЕДИНОЕ ЧИСЛО. То есть, НЕЛЬЗЯ сокращать, например, 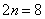на два, получая 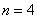. Запись 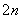лишь обозначает, что количество отрезков чётно. И ни о каких сокращениях речи не идёт

Итак, наше разбиение имеет следующий вид:

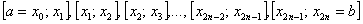
Формула Симпсона для приближенного вычисления определенного интеграла имеет следующий вид:
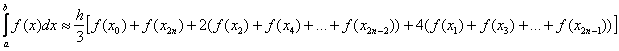, где:
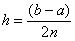– длина каждого из маленьких отрезков или шаг;
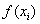– значения подынтегральной функции в точках .

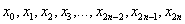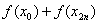– сумма первого и последнего значения подынтегральной функции;
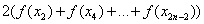– сумма членов с чётными индексами умножается на 2;
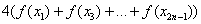– сумма членов с нечётными индексами умножается на 4.

Пример .Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,001. Разбиение начать с двух отрезков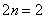

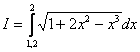
Решение: Начинаем решать. Если у нас два отрезка разбиения 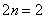, то узлов будет на один больше: 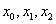. И формула Симпсона принимает весьма компактный вид:

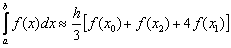
Вычислим шаг разбиения: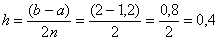

Заполним расчетную таблицу: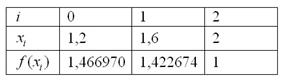
Сколько оставлять знаков после запятой?Действительно, в условии опять об этом ничего не сказано. Принцип тот же, что и в методе трапеций, смотрим на требуемую точность: 0,001. И прибавляем дополнительно 2-3 разряда. То есть, округлять нужно до 5-6 знаков после запятой.

В результате:

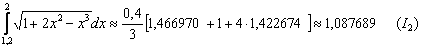
Первичный результат получен. Теперь удваиваем количество отрезков до четырёх: 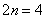. Формула Симпсона для данного разбиения принимает следующий вид: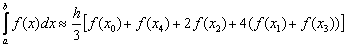

Вычислим шаг разбиения: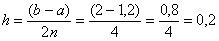

Заполним расчетную таблицу:

Таким образом:

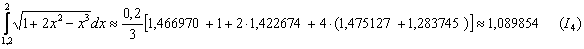
Найдём абсолютное значение разности между приближениями:

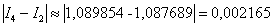
Так как 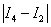больше требуемой точности: 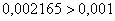, то необходимо еще раз удвоить количество отрезков: .

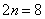Формула Симпсона:

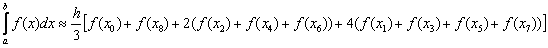
Вычислим шаг: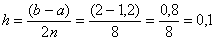

И снова заполним расчетную таблицу:

Таким образом:

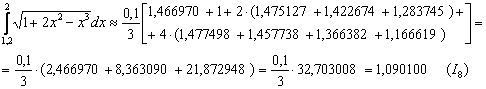
Заметьте, что здесь вычисления желательно уже расписать более подробно, поскольку формула Симпсона достаточно громоздкаОцениваем погрешность:

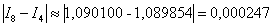
Погрешность меньше требуемой точности: 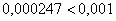. Осталось взять наиболее точное приближение 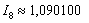, округлить его до трёх знаков после запятой и записать:

Ответ: 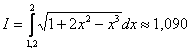с точностью до 0,001