Неопределенный интеграл

Понятие первообразной функции

Функция F(x) называется первообразной функцией (или просто первообразной) функции f(x) на интервале (a; b), если в любой точке x интервала (a; b) функция F(x) дифференцируема и имеет производную F′(x), равную f(x), или дифференциал F′(x)dx= f(x)dx.

Если функция F(x) является первообразной функции f(x) на интервале (a; b), то, очевидно, и функция F(x)+ C, где С – любое постоянное число, также является первообразной функции f(x) на интервале (a; b). Естественно возникает вопрос о том, как связаны между собой различные первообразные одной и той же функции f(x). Ответ на этот вопрос дает следующая теорема.

Теорема 1. Если F₁(x) и F₂(x) – любые две первообразные функции f(x) на интервале (a; b), то всюду на этом интервале F₁(x) - F₂(x) = C, где C- некоторая постоянная.

Следствие.Если функция F(x) является одной из первообразных функции f(x) на интервале (a; b), то любая первообразная Ф(х) функции f(x) на этом интервале имеет вид Ф(х)=F(x)+C, где C- некоторая постоянная.

Неопределенный интеграл

Совокупность всех первообразных функции f(x) на интервале (a; b) называется неопределенным интегралом от функции f(x) на этом интервале и обозначается формулой:

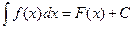(1.1)

В формуле (1.1) знак 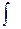называется знаком интеграла, выражение f(x)dx -подынтегральным выражением, сама функция f(x) – подынтегральной функцией, переменная х – переменной интегрирования.

Подчеркнем, что если первообразная функции f(x) на интервале (a;b) (а стало быть, и неопределенный интеграл от этой функции) существует, то в формуле (1.1) подынтегральное выражение f(x)dx равно дифференциалу dF(x) любой из первообразных F(x) функции f(x).

На вопрос о существовании у функции f(x) первообразной и неопределенного интеграла отвечает следующая теорема.

Теорема 2 (Теорема Коши). У любой непрерывной на интервале (a; b) функции f(x) существует на этом интервале первообразная и неопределенный интеграл.

Операция нахождения неопределенного интеграла от функции f(x) называется интегрированием этой функции.

Геометрически неопределенный интеграл представляет собой семейство “параллельных” кривых y=F(x)+C. Каждому значению С соответствует определенная кривая семейства. График каждой первообразной называется интегральной кривой.