Как вычислить определенный интеграл методом трапеций?
Сначала формула в общем виде. Рассмотрим определенный интеграл 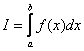 , где
, где 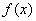 – функция, непрерывная на отрезке
– функция, непрерывная на отрезке 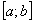 . Проведём разбиение отрезка
. Проведём разбиение отрезка 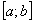 на
на 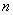 равных отрезков:
равных отрезков:
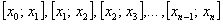 . При этом, очевидно:
. При этом, очевидно: 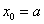 (нижний предел интегрирования) и
(нижний предел интегрирования) и 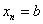 (верхний предел интегрирования). Точки
(верхний предел интегрирования). Точки 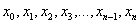 также называют узлами.
также называют узлами.
Тогда определенный интеграл можно вычислить приближенно по формуле трапеций:
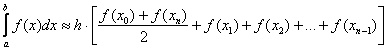 , где:
, где:
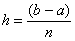 – длина каждого из маленьких отрезков или шаг;
– длина каждого из маленьких отрезков или шаг;
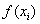 – значения подынтегральной функции в точках
– значения подынтегральной функции в точках 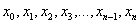 .
.
Пример .Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой. 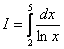
а) Разбив отрезок интегрирования на 3 части.
б) Разбив отрезок интегрирования на 5 частей.
Решение:
а) 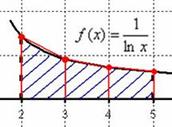
По условию отрезок интегрирования нужно разделить на 3 части, то есть 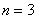 .
.
Вычислим длину каждого отрезка разбиения: 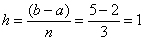 . Параметр
. Параметр 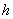 , напоминаю, также называют шагом.
, напоминаю, также называют шагом.
Сколько будет точек 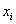 (узлов разбиения)? Их будет на одну больше, чем количество отрезков:
(узлов разбиения)? Их будет на одну больше, чем количество отрезков:
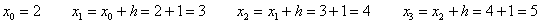
Ну а общая формула трапеций сокращается:
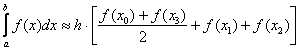
Для расчетов можно использовать обычный микрокалькулятор:
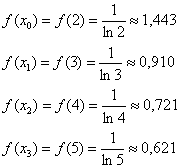
Обратите внимание, что, в соответствии с условием задачи, все вычисления следует округлять до 3-го знака после запятой.
Окончательно:
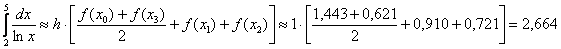
С геометрической точки зрения мы вычислили сумму площадей трёх трапеций (см. рис. выше).
б) Разобьём отрезок интегрирования на 5 равных частей, то есть 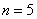 . Зачем это нужно?
. Зачем это нужно?
Если 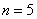 , то формула трапеций принимает следующий вид:
, то формула трапеций принимает следующий вид:
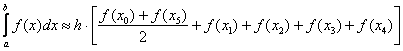
Найдем шаг разбиения:
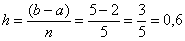 , то есть, длина каждого промежуточного отрезка равна 0,6.
, то есть, длина каждого промежуточного отрезка равна 0,6.
При чистовом оформлении задачи все вычисления удобно оформлять расчетной таблицей:

В результате:
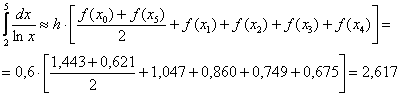
Ну что же, уточнение, и серьёзное, действительно есть! Если для 3 отрезков разбиения приближённое значение составило 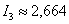 , то для 5 отрезков
, то для 5 отрезков 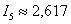 . Таким образом, с большой долей уверенности можно утверждать, что, по крайне мере
. Таким образом, с большой долей уверенности можно утверждать, что, по крайне мере 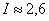 .
.
Дата добавления: 2021-01-26; просмотров: 612;











