Исследование функции методами дифференциального исчисления.

v Интервалы монотонности.

Функция называется возрастающей ( убывающей) в некотором интервале, если в этом интервале каждому большему значению аргумента соответствует большее ( меньшее) значение функции. Как возрастающие, так и убывающие функции называются монотонными.

Правило нахождения интервалов монотонности:

- найти нули и точки разрыва f ’(x);

- определить методом проб знак f ’(x) в интервалах, на которые полученные в п.1 точки делят область определения функции f (x);

- интервалы в которых f ’(x) > 0, являются интервалами возрастания функции, а интервалы в которых f ’(x) < 0, - интервалами убывания функции. При этом если на двух соседних интервалах, граничная точка которых является нулем производной f ’(x), знак f ’(x) одинаков, то они составляют единичный интервал монотонности.

v Экстремум функции.

Точка х = х₀ называется точкой максимума ( минимума) функции y = f(x), если существует такая окрестность точки х₀, что для всех х ( х ¹ х₀) этой окрестности выполняется неравенство:

f(x) < f(x₀), [f(x) > f(x₀)].

Точками максимума и минимума функции называются точками ее экстремума, а значение функции в точке максимума ( минимума) - максимумом ( минимумом) или экстремумом функции.

Правило отыскания экстремумов функции:

- найти нули и точки разрыва f ’(x);

- определить методом проб знак f ’(x) в интервалах, на которые полученные в п.1 точки делят область определения функции f (x);

- из этих точек выделить те, в которых функция f(x) определена и по разные стороны от каждой из которых производная f ’(x) имеет разные знаки – это и есть экстремальные точки; при этом экстремальная точка х = х₀ является точкой максимума если в этой точке происходит смена знака с « + » на « - », и точкой минимума – с « - » на « + ».

v Общая схема исследования функции и построение ее графика.

1. Найти область определения функции.

2. Исследовать функцию на четность или нечетность; проверить так же не является ли она периодической.

3. Найти точки пересечения функции с осями координат.

4. Найти интервалы знакопостоянства.

5. Найти интервалы монотонности, ее экстремумы.

6. Построить график функции, используя полученные результаты.

ПРИМЕР:

Пример 1. Исследовать функцию и построить график.

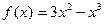
1) Область определения (это множество тех значений, которое может принимать аргумент, т.е. х).

х – любое.

Исследовать функцию у = х² – 5х + 6 и построить ее график.

1. О.о.: х Î (- ¥; + ¥)

2. f( - x) = ( - x)² – 5( - x) + 6 = х² + 5х + 6 Þ функция нечетная; непереодичная.

3. Точки пересечения с осями координат:

- с осью Оу: х = 0, 0² – 5*0+6 = 0 Þ у = 6

- с осью Ох: у = 0 , х² – 5х + 6 = 0

Д = ( - 5)² – 4*1*6 = 25 – 24 = 1

х₁ = 3, х₂ = 2

4. Найдем интервалы знакопостоянства:

У’ = 2x – 5

2x – 5 = 0

x = 2,5

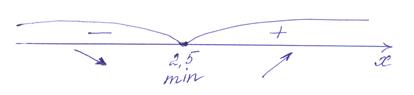
5. Интервалы монотонности:

f( x ) возрастает при х Î ( 2,5; + ¥)

f( x ) убывает при х Î (- ¥; 2,5)

6. Экстремумы:

Х_min = 2,5 Y_min = 2,5² – 5 * 2,5 + 6 = - 0,25

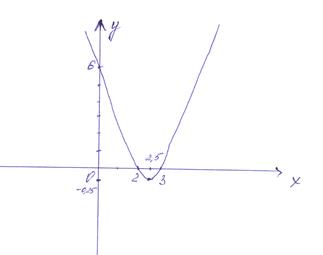
7. График:

7)График.