В. Разностно-дальномерный метод (доплеровский интегральный)
Этот метод основан на измерении разности топоцентрических расстояний между судном и двумя положениями одного и того же НКА в последовательные моменты времени.
В своем движении по орбите НКА последовательно проходит точки S1, S2 и т.д. расстояние между которыми называется базой, длина которой определяется как:
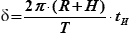
| (23.19) |
| где | tИ – время интегрирования – промежуток времени между двумя последовательными моментами наблюдения НКА. |
Если измерить разность расстояний
| ΔD1 = Di2 − Di1 | (23.20) |
двух последовательных положений НКА, то место наблюдателя окажется на изоповерхности, представляющей собой гиперболоид вращения, фокусы которого совпадают с концами базы, то есть положениями НКА на орбите в моменты начала и конца наблюдений. Гиперболоид образован вращением гиперболы, соответствующей измеренной разности расстояний ΔD вокруг базы и является поверхностью второго порядка.
Пересечение гиперболоида с поверхностью Земли дает изолинию – сложную кривую, близкую по форме к сферической гиперболе. На этой гиперболе и будет находиться судно.
Когда база займет новое положение измеряют вторую разность расстояний
| ΔD2 = Di3 − Di2 | (23.21) |
и получают второй гиперболоид и вторую гиперболу, соответствующую величине ΔD2.
Аналогично можно получить ΔD3 и третью гиперболу и т.д. Место судна получается в точке пересечения 2-х , 3-х и более гипербол.
Разность расстояний ΔDi можно получить подсчетом числа импульсов доплеровской частоты в течении промежутка времени, необходимого НКА для прохождения длины базы. Такой подсчет математически представляет собой интегрирование доплеровского смещения частоты по времени, в результате которого получаем:
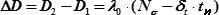
| (23.22) |
где Nσ – подсчитанное число импульсов биений доплеровской частоты.
Таким образом, каждому Nσ соответствует вполне определенное значение разности расстояний от судна до двух последовательных положений НКА на орбите в моменты начала и конца времени tИ – интервала интегрирования.
Постоянная величина δt · tИ – погрешность в определении числа импульсов биений из-за сдвига частоты опорного генератора судового приемоиндикатора.
В этом методе спутниковая РНС аналогична наземной гиперболической РНС.
В судовом ПИ спутниковой РНС «Транзит» были приняты tИ = 2 мин., 1 мин., 30с, 24с. При ΔТИmax = 16 мин. может быть получено соответственно 8, 16, 32 и 40 линий положения.
Так как гиперболы на поверхности Земли пересекаются в двух точках, то определение места судна будет двузначным и разрешение этой двузначности выполняются по счислению пути судна.
В состав судового ПИ входит ЭВМ, так как получаемая от НКА информация не может быть обработана вручную.
В среднеорбитальных СНС при этом методе используются три разности ΔDij = Di − Dj до 4-х НКА, так как при постоянстве D′ за время навигационных определений разности псевдодальностей равны разностям истинных дальностей, для определения которых требуется только три независимых уравнения.
Навигационным параметром является ΔDij. Поверхности положения представляют собой поверхности двухполостного гиперболоида вращения, фокусами которого являются координаты опорных точек i и j (центров масс i-го и j-го НКА). Расстояние между этими опорными точками называется базой. Если расстояния от опорных точек (НКА) до подвижного объекта велики по сравнению с базой, то гиперболоид вращения в окрестностях точки подвижного объекта совпадает со своей асимптотой – конусом, вершиной которого выступает середина базы.
Точность определения места подвижного объекта совпадает с точностью определения этих координат псевдодальномерным способом.
Недостаток разностно-дальномерного метода заключается в том, что в нем не может быть измерено смещение D′, то есть смещение шкалы времени подвижного объекта.
Дата добавления: 2021-01-26; просмотров: 793;











