В завершение главы «интегралы», рассмотрим примеры на комбинацию тем, а именно, кратные несобственные интегралы.

Пример.Найти объём, расположенный под поверхностью 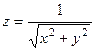над кругом радиуса R.

Вычислится с помощью несобственного двойного интеграла 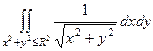. Функция стремится к 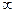в (0,0). Тем не менее, объём конечен, так как в двумерном случае надо перейти к полярным координатам, тогда получается 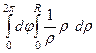, во внутреннем интеграле из-за умножения на якобиан остаётся 1 и в итоге результат 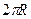, а не .

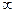Однако в сечении, проходящем через плоскость 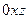, получаем 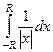, расходящийся интеграл. Да и собственно говоря, в любом сечении, проходящем через ось симметрии, функция минус первой степени 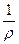. То есть, существует бесконечное число сечений бесконечной площади, притом что объём тела конечен.

Если разбивать на повторные интегралы, то мы столкнёмся с сечением бесконечной площади, т.е. таким способом вычислить этот интеграл будет нельзя, а вот в полярных координатах можно.

Чертежи:

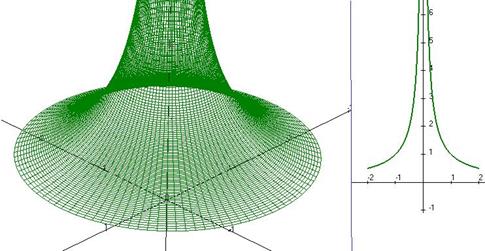
Пример.Вычислить 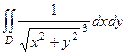где область 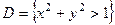, то есть плоскость вне круга радиуса 1.

Решение. = = =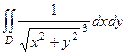

= = = .

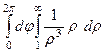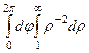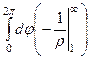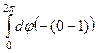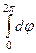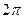ЛЕКЦИЯ № 6. 26.02.2020

Глава 2.

Теория функций комплексного переменного.