Дифференциальные уравнения, допускающие понижение порядка
Простейшим уравнением n-го порядка является уравнение вида
y(n)=f(x)
Его общее решение находится путем n последовательных интегрирований. При каждом интегрировании будет вводиться своя произвольная постоянная, так что решение, как и должно быть, будет зависеть от n произвольных постоянных.
Поясним метод решения примером. Пусть 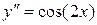 . Тогда
. Тогда 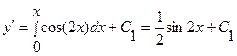 . Интегрируя еще раз, получим
. Интегрируя еще раз, получим 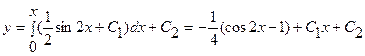 .
.
Если в задаче есть начальные условия, заданные при x=x0, то нижний предел интегрирования удобно брать равным x0. Тогда константы интегрирования находятся особенно просто.
Пусть в нашем примере решение удовлетворяет начальным условиям 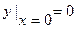 ,
, 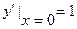 . Тогда из первого условия находим С2=0, из второго – С1=1 , и соответствующее частное решение
. Тогда из первого условия находим С2=0, из второго – С1=1 , и соответствующее частное решение 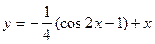 .
.
Для уравнений второго порядка имеются часто встречающиеся на практике частные случаи, когда их интегрирование сводится к последовательному интегрированию двух уравнений первого порядка.
Первый случай. Уравнение не содержит явно искомой функции y, т.е. имеет вид
F(x, y’, y”)=0. (3.4)
В этом случае надо ввести новую неизвестную функцию z=z(x) независимой переменной x, положив y’=z. Тогда y”=z’ и (3.4) принимает вид F(x, z, z’)=0,т.е. оказывается уравнением 1-го порядка относительно z. Решив его, найдем z=j(x,C1), т.е. y’=j(x,C1). Тогда 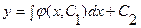 -общее решение уравнения (3.4).
-общее решение уравнения (3.4).
Пример 3.1. Решить уравнение 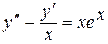 .
.
Рассматриваемое уравнение не содержит искомой функции 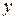 . В результате замены
. В результате замены 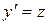 , получим линейное дифференциальное уравнение первого порядка
, получим линейное дифференциальное уравнение первого порядка
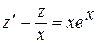 .
.
Его решение есть 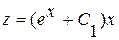 . Тогда
. Тогда
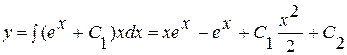 .
.
Второй случай. Уравнение не содержит явно независимой переменной x, т.е. имеет вид
F(y, y’, y”)=0. (3.5)
В этом случае надо за новую независимую переменную принять y, и ввести новую неизвестную функцию z=z(y) переменной y, определенную соотношением 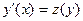 .
.
Тогда 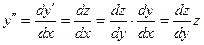 и уравнение (3.5) преобразуется в уравнение 1-го порядка F(y, z,
и уравнение (3.5) преобразуется в уравнение 1-го порядка F(y, z, 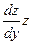 )=0. Решив его, найдем z=j(y,C1), т.е.
)=0. Решив его, найдем z=j(y,C1), т.е. 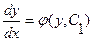 . Разделяя переменные, получим
. Разделяя переменные, получим 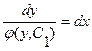 ,
, 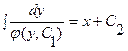 . Это общий интеграл уравнения (3.5).
. Это общий интеграл уравнения (3.5).
Пример 3.2.Решить уравнение 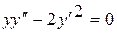 .
.
Данное уравнение не содержит независимый аргумент 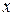 . Полагая
. Полагая 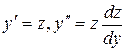 , получим
, получим 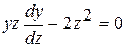 или
или 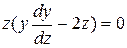 . Это дифференциальное уравнение распадается на два:
. Это дифференциальное уравнение распадается на два: 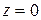 ,
, 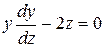 .
.
Первое из них дает 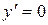 , т.е.
, т.е. 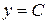 .
.
Во втором переменные разделяются: 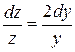 , откуда
, откуда 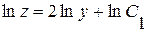 , т.е.
, т.е. 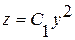 . Т.к.
. Т.к. 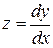 , то
, то 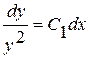 и
и 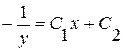 , т.е. (заменяя
, т.е. (заменяя 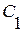 и
и 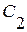 на -
на - 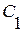 и -
и - 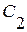 )
)
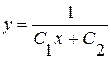 . (3.6)
. (3.6)
Это общее решение нашего дифференциального уравнения. Отметим. что найденное ранее решение 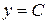 содержится в (3.6), т.к. получается из (3.6) при
содержится в (3.6), т.к. получается из (3.6) при 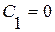 .
.
Линейные уравнения
Дата добавления: 2020-05-20; просмотров: 603;











