Структура общего решения

<6 7 8 91011 12 >

Во многих практических задачах в качестве первого приближения при описании физических процессов возникают линейные уравнения n-го порядка вида

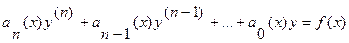(3.7)

Линейными они называются потому, что являются уравнениями первой степени относительно совокупности искомой функции y и ее производных y’, y”,…, y⁽ⁿ⁾. Функции a₀(x), a₁(x), …, a_n(x) называются коэффициентами, а функция f(x) – правой частью уравнения. Все эти функции заданы и непрерывны в той области, в которой рассматривается уравнение (3.7), причем предполагается, что a_n¹0.

В случае, когда f(x) º 0, т.е. когда (3.7) имеет вид

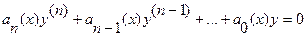, (3.8)

уравнение называется однородным; если же f(x)¹0 – неоднородным.

Оказывается, что линейные уравнения обладают особыми свойствами, которые облегчают нахождение и исследование их решений. Остановимся на некоторых из этих свойств.

Предварительно удобно ввести следующее определение. Функции 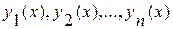называются линейно независимыми на [a, b], если тождество

,

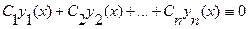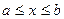
выполняется лишь в случае, когда все постоянные С_i, i=1, …, n равны нулю. Это означает, что ни одна из функций y_i(x) не является линейной комбинацией других на [a, b].

Например, функции e^x, e²^x, e³^x линейно независимы, т.к. выражение С₁e^x+ С₂e²^x + С₃e³^x будет равно нулю только при С₁=С₂=С₃=0. Функции e^x, e²^x, 2e^x не являются линейно независимыми (говорят, что они линейно зависимы), т.к. С₁e^x+ С₂e²^x + 2С₃ 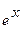º0 при С₁=1, С₂=0, С₃=-1/2.

Упражнение. Сформулируйте условие линейной независимости функций с помощью определителя Вронского .

Имеет место следующая фундаментальная

Теорема 3.1 (о структуре общего решения однородного линейного уравнения). Если функции y₁, y₂ ,…, y_n являются линейно независимыми частными решениями однородного уравнения (3.8), то его общее решение есть

y=С₁y₁+ С₂y₂ +…+ С_ny_n, (3.9)

где C₁,…, С_n – произвольные постоянные.

Совокупность n линейно независимых решений линейного однородного уравнения (3.8) n-го порядка, о которой идет речь в теореме 3.1, называется фундаментальной системой решений этого уравнения.

Заметим, что соотношение (3.9) очень похоже на разложение вектора (элемента линейного пространства) по базису. Это сходство не случайно.

Рассмотрим теперь случай неоднородного уравнения.

Теорема 3.2 (о структуре общего решения неоднородного линейного уравнения). Если функции y₁, y₂ ,…, y_n являются линейно независимы. Если y₀ – общее решение однородного уравнения (3.8), а 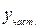- какое-либо частное решение неоднородного уравнения (3.7), то

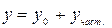(3.10)

есть общее решение неоднородного уравнения (3.7).

Из теорем 3.1, 3.2 следует, что для нахождения общего решения уравнения (3.7) нужно:

1. Найти фундаментальную систему решений y₁, …, y_n соответствующего однородного уравнения (3.8).

2. Найти некоторое частное решение 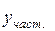уравнения (3.7).

3. Записать общее решение уравнения (3.7) в виде

y=С₁y₁+ С₂y₂ +…+ С_ny_n+ 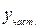. (3.11)

Итак, структура общего решения неоднородного линейного уравнения определяется формулой (3.11).

Замечание. Теоремы 3.1 и 3.2 выражают важный физический принцип суперпозиции.

<6 7 8 91011 12 >

Дата добавления: 2020-05-20; просмотров: 380;