Метод вариации произвольных постоянных
Мы узнали, как решать неоднородные линейные дифференциальные уравнения второго порядка специального вида. Изложим теперь общий метод нахождения решений неоднородных линейных дифференциальных уравнений. Ограничимся, как и прежде, случаем уравнения второго порядка.
Рассмотрим дифференциальное уравнение
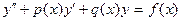 (3.20)
(3.20)
и соответствующее однородное уравнение
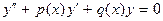 . (3.21)
. (3.21)
Пусть 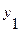 и
и 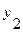 - два линейно независимых решения уравнения (3.21). Тогда общее решение этого уравнения есть
- два линейно независимых решения уравнения (3.21). Тогда общее решение этого уравнения есть
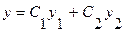 , (3.22)
, (3.22)
где 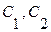 - произвольные постоянные.
- произвольные постоянные.
Попробуем найти такие функции 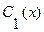 и
и 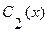 , чтобы при замене
, чтобы при замене 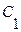 на
на 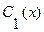 и
и 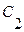 на
на 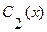 выражение (3.22) удовлетворяло бы нашему неоднородному уравнению (3.20).
выражение (3.22) удовлетворяло бы нашему неоднородному уравнению (3.20).
Так как искомых функций 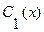 и
и 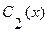 две, а мы наложили на них лишь одно требование: чтобы (3.22) было решением (3.20), то можно подчинить
две, а мы наложили на них лишь одно требование: чтобы (3.22) было решением (3.20), то можно подчинить 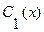 и
и 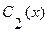 еще одному условию. За такое условие выберем следующее: производная
еще одному условию. За такое условие выберем следующее: производная 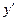 выражения (3.22) должна выглядеть так, как если бы
выражения (3.22) должна выглядеть так, как если бы  и
и 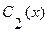 были постоянны, т.е. чтобы было
были постоянны, т.е. чтобы было
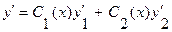 . (3.23)
. (3.23)
Так как на самом деле 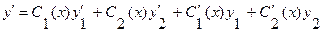 , то условие (3.23) можно записать в виде
, то условие (3.23) можно записать в виде 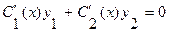 . Тогда
. Тогда 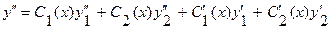 . Подставляя (3.22), (3.23) в (3.20) получим
. Подставляя (3.22), (3.23) в (3.20) получим 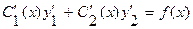 . Таким образом,
. Таким образом, 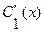 и
и 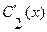 находятся из системы уравнений
находятся из системы уравнений
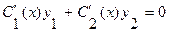 ,
, 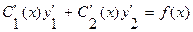 . (3.24)
. (3.24)
Определитель этой алгебраической системы (проверьте, что он является определителем Вронского!) относительно неизвестных 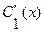 и
и 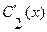 отличен от нуля. Найдя
отличен от нуля. Найдя 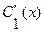 и
и 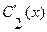 и проинтегрировав их, найдем и функции
и проинтегрировав их, найдем и функции 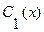 и
и 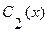 .
.
Описанный метод называют методом Лагранжа (или методом вариации произвольных постоянных).
Пример 3.6.. Найти общее решение уравнения
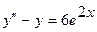 (3.25)
(3.25)
методом Лагранжа.
Решение. Соответствующее однородное уравнение 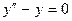 имеет общее решение
имеет общее решение 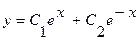 . Решение уравнения (3.25) ищем в виде
. Решение уравнения (3.25) ищем в виде 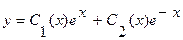 . Система (3.24) принимает вид
. Система (3.24) принимает вид
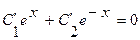 ,
, 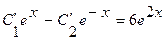 .
.
(Упражнение. Определитель этой системы заведомо отличен от нуля. Почему?) Находим решение системы: 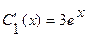 ,
, 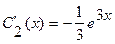 . Тогда
. Тогда 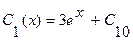 ,
, 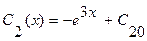 , и общее решение уравнения (3.25) есть
, и общее решение уравнения (3.25) есть 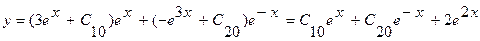 .
.
* Математик второй половины 17-го и первой половины 18-го веков.
Дата добавления: 2020-05-20; просмотров: 574;











