Неоднородные уравнения
Теперь рассмотрим неоднородное уравнение
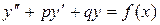 . (3.17)
. (3.17)
Для нахождения общего решения (3.17) нужно, согласно теореме 3.2, найти какое-либо частное решение этого уравнения. Одним из методов нахождения частного решения неоднородного уравнения является метод подбора (иначе, метод неопределенных коэффициентов). Этот метод применим только, когда правая часть f(x) имеет специальный вид
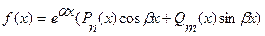 ,
,
символы Pn(x), Qn(x) будем употреблять для обозначения многочленов степени n, 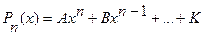 .
.
Мы ограничимся двумя практически важными случаями.
1. Частное решение y* уравнения
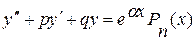
надо искать в виде
(3.18)
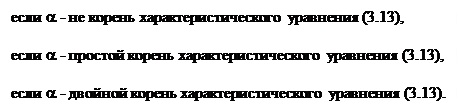
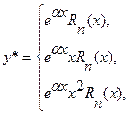
Во всех случаях за Rn(x) нужно взять многочлен степени n с буквенными (неопределенными) коэффициентами, которые определяются после подстановки y* в уравнение (3.17).
2. Частное решение y* уравнения
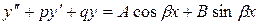
надо искать в виде
(3.19)

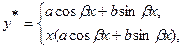 Числа a и b определяются после подстановки y* в (3.17).
Числа a и b определяются после подстановки y* в (3.17).
Пример 3.5. Найти общее решение уравнения 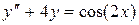 .
.
Решение. Составим характеристическое уравнение однородного уравнения 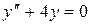 :
: 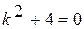 . Найдем его корни:
. Найдем его корни: 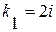 ,
, 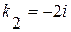 . Общее решение однородного уравнения есть
. Общее решение однородного уравнения есть 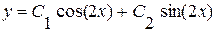 .
.
Частное решение неоднородного уравнения ищем в виде 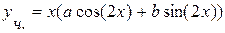 . Находим производные
. Находим производные 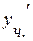 ,
, 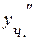 , подставляем
, подставляем 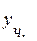 и
и 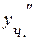 в уравнение
в уравнение 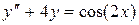 и приравниваем коэффициенты при
и приравниваем коэффициенты при 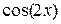 и
и 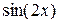 . Получаем систему алгебраических уравнений для определения
. Получаем систему алгебраических уравнений для определения 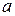 и
и 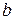 :
: 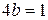 ,
, 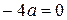 , отсюда
, отсюда 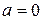 ,
, 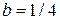 .
.
Итак, общее решение нашего дифференциального уравнения есть 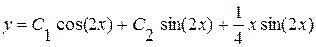 .
.
Дата добавления: 2020-05-20; просмотров: 532;











