Однородные дифференциальные уравнения

Дифференциальное уравнение называется од­нородным, если оно имеет вид

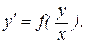(2.19)

В некоторых случаях полезно пользоваться другим равносильным определением однородного дифференциального уравнения. Предварительно отметим следующее. Функция двух аргументов называется однородной степени п,если умножение всех ее аргументов на одно и то же число t равносильно умножению функции на 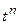, т.е.

.

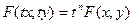Оказывается, что всякая однородная функция F(х, у) степени n представима в виде

.

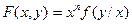С помощью этого свойства можно показать, что определение (2.19) равносильно следующему:

Если в дифференциальном уравнении

P(x,y)dx+Q(x,y)dy = 0 (2.20)

коэффициенты P(x,y) и Q(x,y) – однородные функции одной и той же степени, то уравнение (2.20) называется однородным.

Уравнение (2.19) решается при помощи введении новой неизвестной функции:

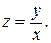(2.21)

В самом деле, из (2.21) следует, что y=zx, откуда y’=z’x+z. Подставляя эти выражения в (2.19), получим z’x+z=f(z) или

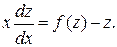
В этом уравнении переменные отделяются:

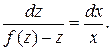
Интегрируя и обозначая 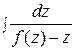через F(z), находим F(z)=lnx+C или, возвращаясь к старой неизвестной функции у, 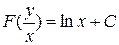. Это общий интеграл нашего дифференциального уравнения.

Пример 2.4.Дифференциальное уравнение

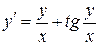
однородное. Подстановка y = zx дает z’x + z = z + tg z откуда

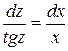
или

.

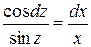Интегрируя, получим ln sin z=ln x+ln C, т.е. sin z = Сx. Отсюда z=arcsinCx и у=х arcsinCx.

Для решения уравнения (2.20) можно поступить двояко: или при­вести его предварительно к виду (2.19), или же сразу применить под­становку (2.20).

Пример 2.5.

(7x²-2xy+6y²)dx+(x²-4xy)dy=0. (2.22)

Первый способ решения. Переписываем уравнение (2.22) так:

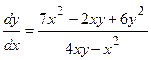
или, деля числитель и знаменатель на ,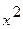

.

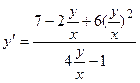Это дифференциальное уравнение вида (2.19), и мы полагаем у=zх. Далее продолжаем, как в предыдущем примере.

Второй способ решения. Делаем подстановку (2.21) непосредственно в уравнении (2.22). Так как y=zx, а dy=xdz+zdx, то получим

(7x²-2x²z+6x²z²)dx + (x²-4x²z)(xdz+zdx) = 0.

Сокращая на х² и делая перегруппировку, имеем

(7-z+2z²)dx + (1-4z)xdz = 0.

Это уравнение с разделяющимися переменными, решать которое мы умеем.