Таким образом, работа расширения

<6 789 10 11 12 >

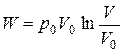Пример 2.8. Пластина из графита толщиной 10 мм на поверхностях имеет постоянные температуры T₁= 1300° С и T₂= 100° С. Найти удельный поток, теплоты q, проходящий через графитную пластину с коэффициентом теплопроводности .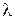

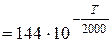Решение. Дифференциальное уравнение переноса тепла (1.3)

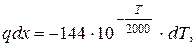
после интегрирования принимает вид

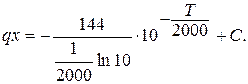(2.26)

Неизвестные C и q находятся из дополнительных условий, соответствующих краевой задаче.

Первое условие: при x = 0 T = T₁ = 1300 ⁰C. Отсюда 0 = 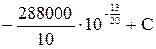и С = 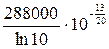. Подставляем значение С в общий интеграл (2.26):

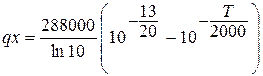Второе условие: при х = 10 мм T = T₂ = 100° С, откуда

q = 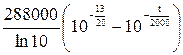= 8,32 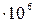ккал/м²ч.

Схема методов интегрирования уравнений первого порядка

В заключение, схематично отразим рассмотренные нами выше методы решения уравнений первого порядка.

Таблица 2.1. Схема интегрирования уравнений первого порядка

Уравнение	Тип уравнения	Метод решения
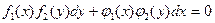
	с разделяющимися переменеными	Разделение переменных и интегрирование

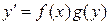
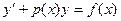
	Линейное 1-го порядка
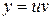
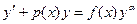.	Уравнение Бернулли
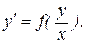
.	Однородное 1-го порядка
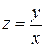
P(x,y)dx+Q(x,y)dy = 0 P(x,y) и Q(x,y) -однородные функции одинаковой степени

1.10. Дифференциальные уравнения высших порядков

Задача Коши

В этом разделе рассматриваются дифференциальные уравнения порядка выше первого

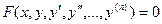(3.1)

Особое внимание мы уделим уравнениям, разрешенным относительно старшей производной, т.е. уравнениям вида

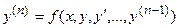. (3.2)

Для дифференциального уравнения (3.2) n-го порядка задача Коши состоит в нахождении такого решения 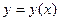уравнения (3.2), которое вместе со своими n-1 первыми производными принимает в заданной точке x₀ заданные значения 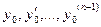, то есть

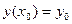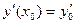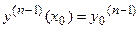, , …, . (3.3)

Условия (3.3) называются начальными.

Вопрос о существовании и единственности решений задачи Коши решает следующая

Теорема 3.1. Если в уравнении (3.2) функция 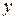и ее частные производные по переменным 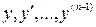непрерывны в некоторой области, содержащей значения 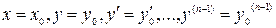, то существует единственное решение этого уравнения 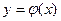, удовлетворяющее начальному условию (3.3).

Если решение уравнения (3.2) зависит от n произвольных постоянных:

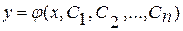, (3.2а)

так что из (4.3а) можно получить любое решение уравнения, то функция (3.2а) называется общим решением уравнения (3.2). Это определение можно уточнить, потребовав единственности решения соответствующих задач Коши, как в случае уравнения первого порядка.

<6 789 10 11 12 >

Дата добавления: 2020-05-20; просмотров: 404;