Линейные дифференциальные уравнения 1-го порядка

Линейным дифференциальным уравнением 1-го порядка называется такое дифференциальное уравнение, в которое неизвестные элементы у и y’ входят в первых степенях, не перемножаясь между собой. Иными словами, это дифференциальное уравнение вида

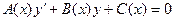. (2.7)

Деля (2.7) на А(х) и полагая для краткости

, ,

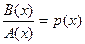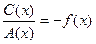придадим (2.7) вид

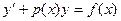, (2.8)

в котором чаще всего и записывают линейное дифференциальное уравнение.

Существует несколько (по существу равносильных) приемов реше­ния линейного дифференциального уравнения. Мы изложим прием Иоганна Бернулли*). Представим (неизвестное нам!) решение у уравнения (2.8) в форме произведения двух сомножителей

y=uv, (2.9)

причем один из них, например v, мы выберем из соображений, связанных с упрощением структуры уравнения (2.8).Подставляя (2.9) в (2.8), находим, учитывая, что :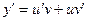

u’v+u(v’+p(x)v)=f(x). (2.10)

Теперь постараемся взять такое v, чтобы ока­залось

v’+p(x)v=0. (2.11)

Для этого надо смотреть (2.11) как на дифференциальное уравнение относительно v и решить его. В (2.11) отделяются переменные 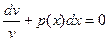. Отсюда .

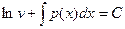Беря С=0 и понимая под 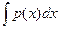какую-нибудь одну пер­вообразную р(х) (этого достаточно, ибо в качестве v мы можем взять любое частное решение уравнения (2.11), кроме v = 0), найдем сначала ln v, а затем и саму функцию v. В результате получится

v=A(x), (2.12)

где А(х) какая-то (известная!) функция. Подставляя (2.12) в (2.10), по­лучим (на основании (2.11)) 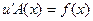. Значит, 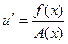, откуда интегрированием найдем u: u=B(x)+C.

Отсюда из (2.9) и (2.12) получаем y=(B(x)+C) A(x).

Изложенный прием с успехом применяется и к так называемому обобщенному линейному уравнению (уравнению Якова Бернулли)

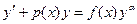. (2.13)

Уравнение (2.13) представляет собой обобщение линейного уравнения (2.8) (последнее получается из (2.13) при ).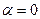

Пример 2.3. Пусть дано дифференциальное уравнение

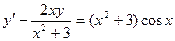. (2.14)

Очевидно, уравнение (2.14) – линейное. Представим решение этого дифференциального уравнения в форме y=uv. Тогда после подстановки этого выражения в (2.14) полу­чится уравнение

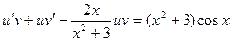
или

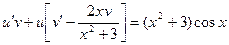. (2.15)

Теперь выберем v таким образом, чтобы коэффициент при u (т. е. выражение, стоящее в квадратных скобках) был равен нулю:

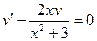. (2.16)

Для этого надо в качестве v взять какое-либо частное решение уравнения (2.16) (кроме решения v=0). Уравнение (2.16) есть дифференциальное уравнение с разделяющимися переменными. Заменяя v’ через 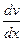и умножая на dx, видим, что отделение переменных достигается делением на v, что дает

.

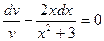Интегрируя, находим

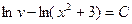. (2.17)

Поскольку в качестве v нам надо взять какое-нибудь одно из ре­шений дифференциального уравнения (2.16), то нет смысла сохранять в (2.17) произвольную постоянную С, а проще придать ей какое-либо определенное значение. Наиболее просто взять С=0, что приводит к выбору

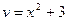. (2.18)

Подставляя это v в (2.15) и учи­тывая (2.16), находим

.

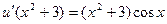Отсюда 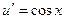и, стало быть, 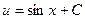(при нахождении 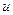произвольную постоянную 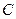уже не фиксируем!).

Отсюда и из (2.18), вспоминая, что y=uv, получим общее решение нашего дифференциального уравнения (2.14):

.

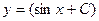
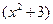Еще раз спросим себя, что привело нас к успешному интегрированию нашего дифференциального уравнения. Вместо исходного сложного уравнения на y мы рассматривали два более простых уравнения на v и u. Этот прием, заключающийся в замене одной сложной задачи двумя (или более) простыми, очень часто используется в математике. Он еще не раз встретится нам в дальнейшем, в частности в следующем разделе.