Уравнения с разделяющимися переменными

Рассмотрим уравнение (2.2)

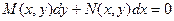. (2.2)

(Далее всюду предполагаем, что функции 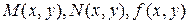непрерывны в некоторой области изменения переменных x,y.)

Уравнение (2.2) (и соответствующее уравнение (2.1)) называется уравнением с разделяющимися переменными, если каждую из функций двух переменных 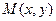, 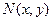при помощи алгебраических преобразований можно представить в виде произведения двух функ­ций, каждая из которых зависит только от одной переменной: , .

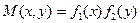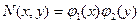Следовательно, уравнение с разделяющимися переменными может быть записано в виде

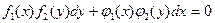. (2.3)

Полагая 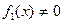, , 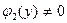разделим обе части (2.3) на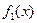 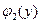. Тогда уравнение (2.3) примет вид

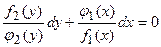. (2.4)

Полученное уравнение (2.4) называют уравнением с разделенными переменными. Интегрируя (2.4) (существование интегралов обеспечено предположением о непрерывности функций):

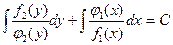, (2.5)

получаем равенство 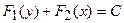, которое можно записать как 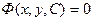. Получен общий интеграл уравнения (2.2).

Если дифференциальное уравнение имеет вид (2.1) и может быть записано в форме

,

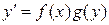то оно является уравнением с разделяющимися переменными. Поясним интегрирование дифференциального уравнения методом разделения переменных примером.

Пример 2.2. Решить дифференциальное уравнение

, .

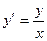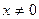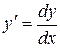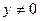Решение. Перед нами уравнение с разделяющимися переменными. Полагаем . При разделяем переменные:

, .

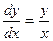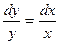Интегрируя обе части последнего равенства, получаем 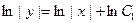. Заметим, что произвольную постоянную С, возникающую при интегрирова­нии, в данном случае удобнее записать в виде 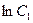(что мы и сделали). Очевидно, что при этом С₁ > 0, но поскольку 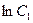изменяется от -¥ до +¥, то постоянная 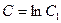может принимать любые значения. Потенцируя полученное равенство, полу­чаем 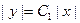или, после раскрытия модуля, 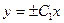. Поскольку величина ±С₁ может принимать любое не равное нулю значение, то решение можно записать в виде 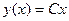, 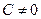. "Потерянное" при разделении переменных решение 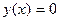(мы предположили, что 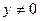) входит в совокупность 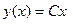при С=0 (а значит, не яв­ляется особым). Таким образом, общее решение рассматриваемого уравне­ния имеет вид 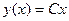, где С может принимать любые значения.

Пример 2.2а.Решить задачу Коши , , .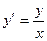

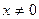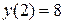Решение. Общее решение уравнения 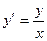имеет вид 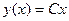. Начальное условие 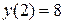выделяет из общего решения некоторое частное. Находим последнее подстановкой общего решения в начальное условие, откуда определяется значение постоянной 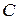: 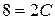, т.е. 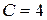. Подставляем теперь найденное значение 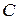в общее решение и получаем искомое решение задачи Коши .

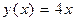Свободное обращение с уравнениями с разделяющимися переменными важно не только потому, что они часто встречаются на практике, но и в связи с тем, к этим уравнениям можно свести решения задач более сложных. Две из них мы сейчас рассмотрим.