Введение в математическое моделирование.

Математическая модель – это приближенное описание какого либо процесса или явления с помощью математических формул. В реальном мире любые процессы или явления бесконечно сложны для понимания. Чтобы описать любой объект, явление или процесс необходимо выявить определяющие его свойства, внутренние связи и закономерности. Роль определяющих характеристик на протекание процесса, поведение объекта или явления. Определить необходимую и достаточную степень точности, необходимую для решения конкретной задачи.

Рассмотрим простую задачу: определение скорости предмета падающего на землю. Что в данном случае является определяющими характеристиками? Еще из школьного курса физики мы помним, что скорость определяется высотой с которой падает предмет и ускорением свободного падения, однако это определение справедливо только для падения в безвоздушном пространстве или при небольших высотах, когда сила трения о воздух имеет очень маленькое значение. В данном случае при построении математической модели (математическом описании процесса) следует учитывать множество исходных данных. Если исходные данные и точность вычисления допускают пренебрежение сопротивлением воздуха то его учитывать нет необходимости, если же нет, то следует учесть при построении модели то, что воздух будет уменьшать скорость падения.

При математическом моделировании изучаемый объект, явление или процесс переводиться на язык математических формул, систем уравнений и неравенств и далее в эту систему вводятся различные исходные данные, сначала контрольные, для определения преемственности модели, а затем неизвестные, для углубления понимания объекта, процесса или явления и прогнозирования.

Процесс построения математической модели объектов состоит из трех этапов. Первый этап состоит в том, что определяются основные свойства и закономерности поведения объекта, процесса или явления. Обычно эти свойства и закономерности строятся на основе предположений или экспериментальных данных.

Следующим этапом производят переложение этих свойств и закономерностей на язык математических формул. Обычно ищут золотую середину, между количеством учитываемых факторов, влияющих на объект, явление или протекание процесса и сложностью составления математических отношений, исходя из того, что все учесть невозможно но необходимо обеспечить достаточную точность работы модели. Кроме того, исходные данные, для построения математической модели в большинстве случаев берут на основе экспериментальных наблюдений, которые как известно содержат определенные погрешности, которые переносятся и на математические соотношения. В результате подобных неточностей, системы уравнений и неравенств моделирующие одни свойства или внутренние взаимосвязи объектов явлений или процессов могут противоречить системам моделирующим другие свойства тех же самых объектов, явлений или процессов. Такие модели естественно пересматриваются.

Последним этапом математического моделирования является решение полученной математической задачи. Решив задачу, необходимо проанализировать полученные результаты и сравнить с их экспериментальными. Если окажется, что результаты вычислений не соответствуют экспериментальным данным, то модель пересматривается. Например, если пользуясь какой либо моделью солнечной системы, мы рассчитываем траекторию полета планеты, и эта траектория не совпадет с той, что окажется в результате наблюдений, то такая модель требует изменений.

В случае успешного тестирования математической модели, на ее основе пишут алгоритм, переводят ее на язык вычислительной техники и далее эти устройства обрабатывают модель с неизвестными параметрами.

Алгоритмизация.

Алгоритмизацией называется процесс разработки алгоритма для решения какой либо задачи. Процесс разработки алгоритма какой либо задачи обычно связан с определенными трудностями. Для примера возьмем задачу: составить алгоритм отыскивания максимального числа среди последовательности из N чисел. Подобные задачи зачастую носят только психологические трудности, «что выбирать? Посмотрел и выбрал», при этом редко задумываемая о том, как мы это делаем. Хотя алгоритм решения очень простой:

1. Считаем что максимальным является первое число;
2. Сравниваем то число, которое считаем максимальным со следующим, и если оно окажется больше, то считаем что максимальным стало следующее число;
3. Повторяем второй пункт до тех пор пока не переберем все числа.

По окончании перебора получим максимальное число в заданной последовательности.

Разработчик алгоритма, точно должен представлять себе алгоритмическую систему в которой разрабатывается алгоритм, то есть набор типов исходных и результирующих объектов, а так же методов и средств их обработки, описанных на языке понятном исполнителю.

Разработка алгоритма неразрывно связана с математическим моделированием. То есть алгоритм решения задачи, это заключительная фаза математического моделирования. Этот процесс отражен на рисунке 10.

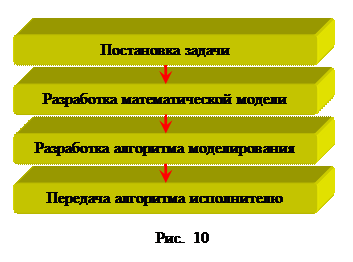
Первый необходимый этап алгоритмизации это содержательный анализ задачи. На этом этапе необходимо определить исходные данные, точнее их типы и типы конечного результата, и кроме того множество допустимых данных, для разрабатываемого алгоритма, для обеспечения его массовости. Другими словами на первом этапе необходимо определить алгоритмическую систему и проанализировать ее возможности и пригодность для решения поставленной задачи с требуемой точностью.

Вторым этапом алгоритмизации является построение математической модели поставленной задачи, то есть перевод задачи на язык математических формул.

Третьим этапом идет разбивка математической модели на шаги, которые предусмотрены в выбранной алгоритмической системе.

И последним этапом алгоритмизации идет процесс разработки пошаговых правил, то есть перевод пошагового выполнения модели на язык понятный исполнителю.

Пример 1.

Рассмотрим процесс алгоритмизации на том же примере поиска максимального числа из последовательности из N чисел.

Определимся с алгоритмической системой. Для этого, проанализируем исходные данные, исходными данными у нас будут представлены как:

1. N - количество элементов последовательности. В качестве типа объектов, представляющих исходных данных определяем множество целых чисел. Сразу заметим, что количество должно быть положительным, то есть строго больше нуля.
2. M – сама последовательность чисел. В качестве типа объектов, представляющих исходных данных определяем множество вещественных чисел.

Далее определимся с результатами, которые будут получены в процессе выполнения алгоритма результаты выполнения алгоритма у нас будут представлены как:

1. M_max – максимальное число из заданной последовательности.

Свойства исполнителя, такие как инструменты и язык пока учитывать не будем.

Построим математическую модель, то есть опишем процесс поиска языком математических формул:

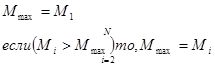
Математическая модель процесса поиска максимального числа из последовательности вещественных чисел M размерностью N построена.

Разрабатываем алгоритм в виде описательных инструкций:

1. Начало алгоритма;
2. Получить количество элементов последовательности N и саму последовательность M.
3. Присвоить значению M_max, значение элемента последовательности M₁.
4. Присвоить счетчику элементов i – значение равное двум. Начинаем перебор со второго элемента, так как первый у нас уже и так считается максимальным.
5. Если не дошли до конца массива, то есть i<=N, то:
1. Если M_i > M_max, то считаем это элемент максимальным M_max = M_i.
2. Переходим к следующему элементу, для этого увеличиваем значение номера элемента i на единицу.
3. Переходим к пункту 5.
6. Записываем результат работы алгоритма M_max;
7. Конец алгоритма.

Итак, мы разработали алгоритм, с помощью которого можно найти максимальное число в последовательности M имеющей количество элементов N.

Следующим этапом идет проверка правильности работы алгоритм. Для этого возьмем произвольную последовательность {1,6,2} размерностью 3 и «проиграем» этот алгоритм пошагово, заранее зная ответ (M_max=6):

ü Начало алгоритма;

ü Получаем количество элементов последовательности N=3 и саму последовательность M={1,6,2};

ü Присваиваем M_max значение первого элемента M_max= M₁=1;

ü Присваиваем счетчику элементов значение номера второго элемента i=2;

ü Не дошли до конца последовательности? 2<=3? «да»;

ü Сравниваем текущий элемент с максимальным M_i> M_max? или 6>1? «да», значит тот элемент который мы считали максимальным таковым не является. Теперь будем считать максимальным второй элемент последовательности M_max= M_i= M₂=6;

ü Увеличиваем значение счетчика элементов на единиц i=i+1, то есть теперь значение счетчика равно 3;

ü Не дошли до конца последовательности? 3<=3? «да»;

ü Сравниваем текущий элемент с максимальным M_i> M_max? или 2>6? «нет», не выполняем никаких действий;

ü Увеличиваем значение счетчика элементов на единиц i=i+1, то есть теперь значение счетчика равно 4;

ü Не дошли до конца последовательности? 4<=3? «нет»;

ü Записываем результат работы алгоритма. На данном шаге получили, что M_max=6.

ü Конец алгоритма.

В результате пошагового выполнения алгоритмы мы получили то же саамы ответ, что и знали заранее, следовательно алгоритм работает правильно и его можно использовать для других последовательностей.

Следующим этапом построения алгоритма, является подготовка его для передачи на дальнейшую обработку, то есть для перевода на язык исполнителя. Для этого создаем его графическое представление, или блок-схему, рисунок 11.

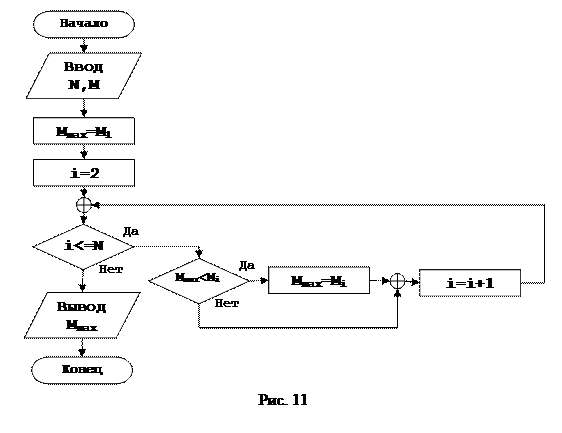
Итак, задание по разработке алгоритма, поиска максимального числа из последовательности чисел размерности N выполнено.