Анализ устойчивости дискретных систем.

Рассмотрим вопрос исследования устойчивости при описании дискретных систем уравнениями состояния. Устойчивость определяется характером собственных движений дискретной системы, т.е. характером движений под действием только ненулевых начальных условий. Если входное воздействие отсутствует, уравнение состояния (63) принимает вид

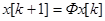(66)

Общее решение системы уравнений (66)

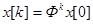
Устойчивость системы (66), а следовательно, и исходной неоднородной системы (63) определяется собственными числами матрицы Ф , т.е. корнями характеристического уравнения

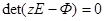(67)

Если все корни 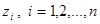удовлетворяют условию

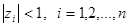
то система устойчива. Если существует хотя бы один корень такой, что 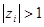, то импульсная система, описываемая уравнением (63), неустойчива. Случай, когда 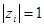, является критическим. При этом система устойчива, если данный корень имеет первый порядок кратности.

При использовании математического описания импульсных систем в терминах пространства состояний оказывается возможным применить простой и удобный в вычислительном отношении критерий устойчивости. Справедливы утверждения:

Если все корни характеристического уравнения (67)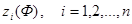

,удовлетворяют условию

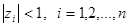(68)

то

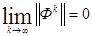(69)

При этом в уравнении (69) может использоваться любая из известных форм нормы матрицы. Справедливо и обратное утверждение, т.е. из условия (69) следует условие (68).

2. Если 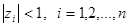(70)

и кратные корни на единичной окружности отсутствуют, то

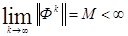(71)

и обратно, выполнение условия (71) влечет за собой выполнение условия (70).

3. Если существует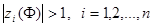

или имеются кратные собственные числа матрицы Ф , принадлежащие единичной окружности, то

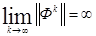
Справедливо также и обратное утверждение.

Таким образом, исследование устойчивости может производиться по анализу элементов матрицы при . Обычно рассматривают последовательность матриц

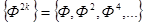
(эта последовательность просто формируется с помощью ЭВМ), задаются малым числом и достаточно большим числом и с помощью ЭВМ проверяют выполнение одного из условий

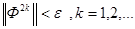
или

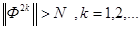
В первом случае соответствующая импульсная система устойчива, во втором случае она неустойчива. Возможна модификация этого алгоритма на основе привлечения ум оценки неустойчивости следов матрицы 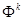при 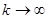, IIpи используется следующее утверждение :если существует такое k , что

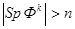
где n - порядок системы, то среди собственных чисел матрицы имеется хотя бы одно 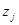, удовлетворяющее условию 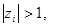и тогда импульсная система неустойчива. Справедливость этого утверждения следует из равенства

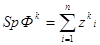
Очевидно, что если все собственные числа матрицы удовлетворяют условию

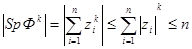(72)

поэтому нарушение условия (72) влечет за собой появление собственного числа, определяющего неустойчивость системы.