Геометрическое моделирование и синтез форм деталей

Геометрическая модель – совокупность сведений, однозначно определяющих форму геометрического объекта. Геометрические модели могут быть представлены совокупностью уравнений линий и поверхностей, алгебраическими соотношениями, графиками, списками, таблицами, описаниями на специальных графических языках. Теоретической основой создания геометрических моделей являются аналитическая геометрия, теория графов, алгебра логика.

При геометрическом проектировании геометрические модели применяются для описания геометрических свойств объекта конструирования (формы, расположения в пространстве); решения геометрических задач (позиционных и метрических); преобразования формы и положения геометрических объектов; ввода графической информации; оформления конструкторской документации. Различают геометрические модели: аналитические, алгебрологические, канонические, рецепторные, каркасные, кинематические и геометрические макромодели.

Аналитические геометрические модели представляются уравнениями, описывающими контуры или поверхности детали. Например, общее уравнение кривой второго порядка на плоскости в прямоугольной системе координат

F (x, y)= ax² + 2bxy + cy² + 2dx + 2ey + g = 0. (3)

Поверхность вращения описывается уравнением

F (x, y, z) = a (x² + y²) + bz² + 2cz + d = 0, (4)

где x, y, z – оси координат; a, b, c, d, e, g – постоянные коэффициенты.

Аналитические модели (3, 4) служат основой для описания элементарных геометрических объектов, на базе которых могут быть получены составные геометрические объекты.

Алгебрологические геометрические модели обеспечивают задание плоских фигур и трехмерных тел, в которых геометрический объект описывается логической функцией условий, выражающих принадлежность точки тем или иным пространственным областям.

Пусть области D₁ -D₄ на плоскости xоy (рис. 16) определены с помощью неравенств следующим образом:

D₁: x ≥ - 6, x ≤ 6, y ≤ 6, y ≥ - 6;

D₂: x ≥ 0, x ≤ 10, y ≥ 0, y ≤ 9; (5)

D₃: (x - 6)² + (y + 6)² ≥ 36;

D₄: y ≤ (x + 6).

Тогда геометрический объект D₀ может быть записан с помощью соотношений (5) и логического выражения

(D₁ ∩ D₃) U (D₁ ∩ D₄) U D₂ (6)

Таким образом, соотношения (5) и (6) определяют алгебрологическую модель геометрического объекта D₀.

Канонические геометрические модели применяют в тех случаях, когда в геометрических объектах удается выделить параметры, которые однозначно определяют их форму. Например, для окружности такими параметрами являются координаты центра и радиус окружности.

Рецепторные геометрические модели в своей основе имеют приближенное представление геометрического объекта в плоскости или пространстве рецепторов (индикаторных функций). В области рецепторов строится прямоугольная решетка или сеть.

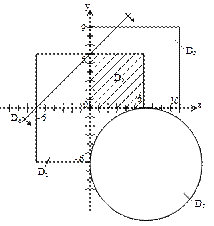
Рис. 16. Графическое представление алгебрологической модели объекта D₀ на плоскости

Каждая клетка сети или решетки рассматривается как отдельный рецептор, который может иметь состояние 0 или 1. Рецептор считается активным (значение 1), если он включается в контур плоской или пространственной области.

Каркасные геометрические модели используют при описании поверхности в прикладной геометрии. При этом одним из основных понятий является понятие определителя поверхности. Определитель поверхности включает совокупность условий, задающих поверхность. Определитель поверхности состоит из геометрической и алгоритмической частей. В геометрическую часть входят геометрические объекты, а также параметры формы и положения; алгоритмическая часть задаётся правилами построения точек и линий поверхности при непрерывно меняющихся параметрах геометрической модели.

3.10. Оценка результатов конструкторского проектирования
на основе функциональных моделей

Конструкция машины как объекта проектирования представляет собой сложную систему. Математическое описание конструктивных элементов прежде всего базируется на блочно-иерархическом подходе к процессу конструирования (рис. 17). Для технологических машин характерны следующие иерархические уровни: система машин – агрегат – узел – деталь. Уровень IV (низший уровень) составляют детали машин, уровень III – совокупность деталей – узел (сборочная единица), уровень II – агрегат – совокупность узлов, уровень I – совокупность машин (агрегатов). Соответственно иерархии объектов проектирования можно построить иерархию их математических моделей (ММ). Выходными параметрами деталей является статические параметры, например, геометрические параметры, которые будут внутренними при проектировании узлов. В свою очередь, типичными выходными параметрами узлов являются динамические параметры, определяющие качество движения (скорости, ускорения, частоты, амплитуды колебаний и т.д.). Выходные параметры агрегата – параметры, характеризующие качество выполнения операций, например, загрузки детали промышленным роботом в станок ЧПУ. Система машин характеризуется параметрами технологического процесса, состоящего из операций, выполняемых отдельными машинами и агрегатами.

ММ на микроуровне (модели деталей) чаще всего строятся на основе дифференциальных уравнений в частных производных. Решение этих уравнений осуществляется методами конечных элементов или конечных разностей. В результате решения уравнений ММ могут быть получены параметры искажения формы деталей под воздействием силовых, тепловых, вибрационных и других внешних нагрузок. Внутренними параметрами на микроуровне будут параметры материала деталей и их формы. К ММ в виде уравнений в частных производных сводятся также задачи расчета упругих (кручение и изгиб) и тепловых деформаций валов и корпусных деталей станков и машин.

Анализ узлов с позиции функционального проектирования основан на ММ макроуровня, выражаемых системами ОДУ. Примеры узлов: приводы подач рабочих органов станков и машин, механизм главного движения станков и т.д. Цель анализа динамики машин и станков – оценка их устойчивости и качества.

При моделировании станков и машин на уровне агрегатов большое внимание уделяется изучению и определению динамики их несущих систем. В этом случае основными внутренними параметрами узлов является жесткость, масса и демпфирование, а внешними параметрами – переменные нагрузки и воздействия на конструктивные узлы (технологические усилия, силы трения, параметрические воздействия). Модели машин на уровне агрегатов представляются многомассовыми системами и описываются системами дифференциальных уровней. Одна из важных форм представления этой системы следующая:

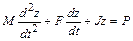, (7)

где z – вектор перемещений; M – матрица масс; F – матрица демпфирования; J – матрица жесткости; P – вектор нагрузок.

Решение системы (7) применительно к металлообрабатывающему станку позволяет определить относительные колебания инструмента и детали под воздействием сил резания.

Математические модели систем машин и станков служат для расчета производительности, надежности и экономической эффективности технологических систем в целом. Анализ качества таких систем выполняется на метауровне с помощью их имитационного моделирования как систем массового обслуживания. Составление имитационной модели производится по структурной схеме системы.