Вопрос 2. Прием дискретных с-лов в каналах с замираниями.
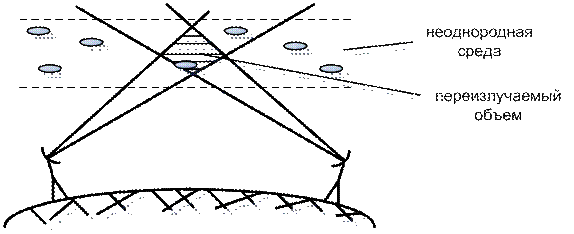
Рис. Рассеяние и переизлучение с-ла в среде.
 Каналы со случайными параметрами и свободно распространяющимися сигналами (кроме фазы, флуктуирует амплитуда)
Каналы со случайными параметрами и свободно распространяющимися сигналами (кроме фазы, флуктуирует амплитуда)
I гр.
Существует геометрическая видимость передатчик – приемник.
Случайные измен. пар-ров среды приводят к var коэф. передачи канала и времени распространения с-ла.
Var пар-ры среды медленно и можно считать const за время сеанса, но от сеанса к сеансу var случайным образом.
Запас мощности передатчика, смена раб. ч-т, уменьшение скорости передачи à поддерживает треб. верность передачи.
Геометрическая видимость передатчик – приемник отсутствует. Связь обеспечивается за счет отражения и рассеивания с-ла локальными неоднородностями среды распространения (см. рис. ). Появление неоднородностей – рез-т действия быстро изменяющихся случайных факторов (вихревые процессы, физико-химические превращения и др. уменьшаются).
Рез-т à излученный с-л попадает на вх. приемника по многим путям (многопутевое распространение, многолучевость). На вх. приемника ∑ отдельных колебаний, время и амплитуда которых случайны. Возникает интерференция и как следствие «замирания».
Для оптим. приема надо знать хар-р поведения их огибающей и фазы.
Полагают, что за время, равное длительности посылки с-ла структура среды не успевает существенно измениться. à у суммарного с-ла на вх. приемника амплитуда и фаза в пределах длительности одной посылки остаются ≈ постояннными и изменяются от посылки к посылке. Амплитуда меняется медленнее чем фаза.
Статистические св-ва огибающей сигнала в канале с замираниями описывают с помощью ф-ции распределения. Чаще всего для этого исп. з-н Рэлея.
Т.к. амплитуда вх. с-ла С.В., то hx2 и pош(hx2) – тоже С.В. à необходимо усреднить pош(hx2) по всем возможным значениям hx2. С исп. Рэлеевского распределения
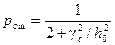
h02 – энергетическое отношение с-л/шум без учета случайных параметров среды;
γc2 – постоян. коэф., зависит от класса рассматриваемх двоичных с-лов.
При одной и той же ср. мощности передатчика помехоустойчивость в канале с замираниями существенно ниже (хуже), чем в канале с постоянными параметрами.
Например, для достижения pош = 10-5 в канале с релеевскими замираниями необходимо увеличить мощность по срав. с каналом без замираний ≈ 4500 раз.
Основ. способ увеличения помехоустойчивости – разнесенный прием.
Суть – решение о переданном символе производится не по одному, а по нескольким, несущим одно и то же сообщение с-лам.
Варианты:
А. Частное разнесение – одновременно передавать не нескольких частотах.
Б. Временное раснесение – повторение несколько раз через определенные промежутки времени.
В. Пространственное разнесение – от одного передатчика принимать сразу на несколько антенн, расположенных на некотором расстоянии друг от друга.
Г.
Д.
……и т.д.
- по углу прихода луча;
- по поляризации;
- по времени запаздывания…
Общее требование к разнесенному приему: чтобы взаимная корреляция замираний в ветвях (разнесения) была незначительной.
à с увеличением числа ветвей разнесения увеличивается вер-ть того, что хотя бы в одной ветви амплитуда с-ла окажется достаточно большой, чтобы обеспечить треб. верность передачи.
Но увеличение числа ветвей до 3 шт существенно уменьшает рош, увеличение числа ветвей до 4 шт и более не существенно снижает рош.
Тема 5. Прием сигналов в системах передачи дискретных сообщений.
Лек. 12. Реальные способы приема дискретных сигналов.
1. Прием частотно-манипулированных с-лов.
2. Прием фазо-манипулированных с-лов.
3. Прием с-лов с относительной ФМн.
3.1. Суть метода.
3.2. Сх. реализация когерентного метода.
3.3. Сх. реализация автокорреляционного метода.
3.4. Срав. оценка помехоустойчивости оптимальных и реальных методов приема с-лов.
Оптимальные сх. приема реализуют предельное превышение с ФНн с-ла над помехой, обеспечивая максимальную (потенциальную) помехоустойчивость с-м связи при когерентной и некогерентном приемах с-лов. Однако реализация оптимальных приемников на практике явл. весьма сложной технической проблемой.
«Отступления от оптимальных сх. приема» на практике позволяют исп. более простые и дешевые схемы, учитывающие ряд факторов инженерного характера. Тем не менее при этом удается не очень ухудшить их качественные показатели по сравнению с соответствующими оптимальными приемниками.
 Реальные способы приема (как и оптимальные)
Реальные способы приема (как и оптимальные)

 Когерентный прием Некогерентный прием
Когерентный прием Некогерентный прием

 АМн ЧМн ФМн АМн ЧМн ФМн
АМн ЧМн ФМн АМн ЧМн ФМн
Обычно не используются, т.к. схемы значительно сложнее, чем некогерентного приема если идти на усложнение, то целесообразно исп.
Ограниченное применение пассивная пауза bS = 0, 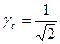
Вопрос 1. Прием ЧМн
Для передачи двоичной цифровой инф.
S0(t) = Acos(ω0t + φ0)
S1(t) = Acos(ω1t + φ1)
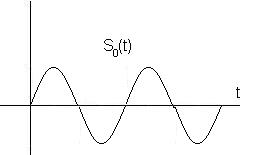
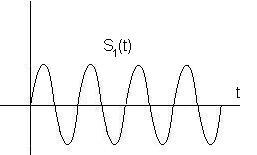
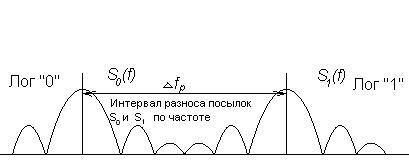
Рис. Временная диаграмма и спектр ЧМн с-лов.
Реальный прием простых двоичных с-лов осуществляется схемами, в которых основ. фильтрацию с-ла от помехи выполняет квазиоптимальный фильтр, а отчет в конце интервала анализа берется по огибающей вых. колебания.
Квазиоптимальный фильтр – линейный фильтр, частотные и фазовые хар-ки которых заданы или выбраны заранее.
Может «квази» = «почти» = «близкий».
Уменьшается полосы пропускания приемника à уменьшается мощность помех, дальше уменьшается полоса пропускания приемника, начинается уменьшение энергии полезного сигнала.
à Для квазиоптимального фильтра оптимальная полоса ч-т, при которой отношение с-л/шум = max.
Впервые такой фильтр исследовал В.И.Сифоров:
Прохождение одиночного радиоимп. с прямоугольной огибающей в присутствии аддитивного белого шума
а) идеальный полосовой фильтр max с-л/шум при Δf ≈1,37/T, h12 = 0,825 h02, где h02 – max с-л/шум при оптимальной обработке;
б) квазиоптимальный (одиночный колебат. контур) –“– Δf ≈1,37/T, h12 = 0,825 h02
Вывод. Квазиоптимальные фильтры:
1) обеспечивают помехоустойчивость ≈ ту же, что и оптимальные сх. (на фоне флуктуационных помех);
2) малокритичны к небольшим отклонениям ч-ты;
3) не критичны к отклонениям фазы принимаемого с-ла.
Если идет прием не одиночного с-ла, а непрерывной последовательности имп., то имеют место остаточные колебания от предыдущих, т.е. следует учитывать взаимное перекрытие. Для этого случая
Δfэф. опт = 1,1/Т; h12 = 0,58 h02 (5.29)
На практике для реальных схем обычно полагают
Δf = 2/Т; h12 ≈ 0,5 h02.
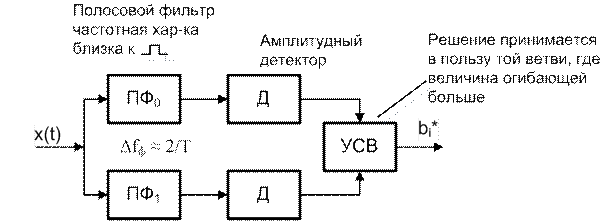
Рис. Структурная сх. некогерентного приема ЧМн с-ла (вариант).
Помехоустойчивость УМн с-лов:
1) При оптим. когерентном приеме  см. (5.24)
см. (5.24)
2) При оптим. некогерентном приеме 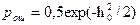 см. Л.11, в-с 1
см. Л.11, в-с 1
3) При приеме по по огибающей 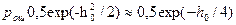 см. (5.29)
см. (5.29)
с помощью полосовых фильтров
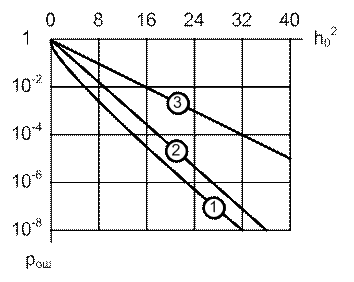
Рис. Помехоустойчивость ЧМн с-лов при различных способах приема.
Анализ графиков и формул:
1) помехоустойчивость (pош) оптимального некогерентного приема несущественно отличается (хуже) от оптимального когерентного.
2) реальный приемник с ПФ по срав. с оптим. некогерентным дает 2-х кратный проигрыш по мощности.
Вопрос 2. Прием ФМн с-лов.

 S(t) = Acos(
S(t) = Acos( 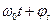 ) :
) : 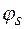
Алгоритм оптим. обработки равновероятных и имеющих одинаковую энергию двоичных с-лов.
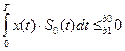
Т.к. с-лы при ФМн противоположны, то S0(t) = – S1(t), то
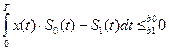
Напряж. на вых. фазового детектора имеет вид линейно-нарастающих имп., полярность которых определяется значением разности фаз опорного и принимаемого колебания.
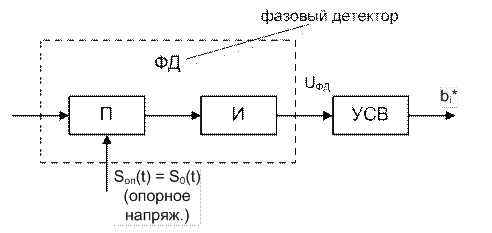
Рис. Структурная сх. приемника ФМн с-лов.
Если напряж. на вых. ФД в момент окончания посылки с-ла положительно, то УСВ принимает решение в пользу b0.
Но чтобы вых. напряж. ФД зависело телько от значения фазы с-ла Sоп(t) должно быть: 1) синхронным с принимаемым с-лом; 2) начальная фаза должна быть равна 0.
ФД синхронный (когерентный)
 (пути реализации – решения)
(пути реализации – решения)
Исп. местного высокостабильного генератора Sоп(t), фазируемого с Sоп передатчика в начале каждого сеанса связи. Сложно, например относит. нестабильность ч-ты df/f = 10-6…10-8 можно только в течении (2·103 ÷ 20) с.
Формирование опор. напряж. из с-ла, принимаемого совместно с помехами. Повсеместно исп. на практике. УФОН (уст-во формирования опорного напряж.) работает по принципу снятия манипуляции с ФМн с-ла и фильтрация полученного напряж. от помех.
Основной недостаток с-м с ФМн à явление обратной р-ты ФД. à
Если нач. фаза φоп изменит «вдруг» свое знач. на +180º или на –180º, то полярность напряж. на вых. ФД UФД соответствующая посылкам S0 и S1 изменится на обратную). à
Устраняется в с-мах с ОФМн, относительной фазовой Мн сов. уч. Н.Т. Петрович, 1954г.
Вопрос 3. Прием с-лов с ОФМн.
3.1. Суть метода ОФМн: выбор фазы сигнальной посылки зависит не только от вида информационного символа (0 или 1), подлежащего передаче, но и от того, какой была фаза предыдущей посылки (0 или 180º).
Вариант (один из двух): При передаче символа лог. «0» фаза посылки остается такой же, как и у предыдущей посылки, а при передаче символа лог. «1» фаза посылки изменяется на 180º по отношению к фазе предыдущей посылки.
| Кодовые символы | |||||||||||||
| φS ФМн | 180º | 180º | 180º | 180º | 180º | 180º | |||||||
| φS ОФМн | 180º | 180º | 180º | 180º | 180º | 180º |
Схемная реализация ОФМн требует элемент памяти (ЭП) для учета «ситуации» по предыдущему символу.
Схемная реализация наиболее распространена:
1) когерентный метод (метод сравнения полярностей);
2) автокорреляционный метод (метод сравнения фаз).
3.2.

Рис. Структурная сх. приемника ОФМн с-лов
(сравнение полярной – когерентный метод)
ФД осуществляет демодуляцию ОФМн с-лов на его вых. положит. или отрицательные видеоимпульсы.
УСВ – сравнивается полярность огибающей принятой посылки с полярностью огибающей предыдущей посылки.
+ Ошибки от явления «обратной р-ты» ФД при переноске фазы φоп на ± 180º охватывает один или max два.
– Если ошибка, из-за действия помех и на вых. ФД полярность изменится, то она всегда парная, т.е. на 2 символа (на ошибочно принимаемый и на следующий).
3.3.
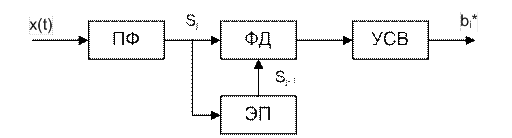
Рис. Структурная сх. приемника ОФМн с-лов
(сравнение фаз – автокорреляционный метод).
В качестве опорного напряж. исп. предыдущая посылка с-ла, которая запоминается на время τ = T.
ФД сравнивает фазы принятой посылки с фазой предыдущей (опорной) посылки. На вых. ФД положит. или отрицат. полярности с-л.
+ Принципиально исключает возможность обратной р-ты ФД.
3.4. Сравнит. оценка помехоустойчивости оптимальных и реальных методов приема простых с-лов с ФНн для реальных схем путем замены в теоретических вместо 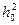 на
на 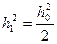 .
.

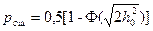 - оптимальный приемник;
- оптимальный приемник;
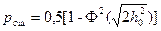 - метод сравнения полярностей (когерентный метод);
- метод сравнения полярностей (когерентный метод);
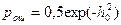 - метод сравнения фаз (автокорреляционный метод);
- метод сравнения фаз (автокорреляционный метод);
 1 оптимальный приемник ФМнС
1 оптимальный приемник ФМнС
2 прием ОФМн по методу сравнения
полярностей (когеренный)
3 прием ОФМн по методу сравнения
фаз (автокорреляционный)
4 реальный прием ОФМнС по методу
срав. полярностей
5 реальный прием ОФМнС по методк
срав. фаз
Рис. Помехоустойчивость ФМн и ОФМн
с-лов при различных способах приема.
В реальных приемниках для ↓ влияния помех обычно исп. фильтры с полосой пропускания Δf = 2/т. Кроме того в ех. ФД идеальный интенограф чисто заменяют фильтром нижних ч-т (ФНЧ) с полосой пропускания Δfφ ≈1/т. Применение этих ФНЧ эквивалентно тому, что шумовая полоса до ФД Δfэ будет равна 2 Δfφ или 2/т.

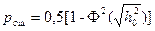 - метод срав. полярностей;
- метод срав. полярностей;
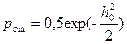 - метод срав. фаз.
- метод срав. фаз.
Относительные методы могут успешно приниматься не только в с-мах с ФМн, а также в с-мах с ЧМн и АМн. особенно эффективно их приминение в каналах в замираниями.
Дата добавления: 2016-06-29; просмотров: 1715;











