Деформации и перемещения бруса

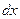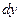Рассмотрим прямой брус (рис.7.4,а). От действия нагрузок этот брус деформируется, то есть изменяет свою начальную форму и размеры. Возьмем произвольную точку абруса в плоскости xоy(горизонтальная плоскость, которая проходит через ось бруса) и проведем из этой точки два взаимно перпендикулярные бесконечно малые отрезки, длины которых до загружения бруса равны и (рис. 7.6).

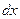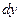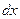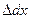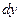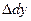После нагружения бруса, точка апереместится в положение а′.Длины отрезков и получат некоторые приращения положительного или отрицательного знаков и станут равными + и + соответственно. Изменится также угол между этими отрезками. Он станет острым или тупым. Величина 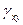, на которую изменится начальный угол между проведенными отрезками,, называется относительной угловой деформацией или относительным сдвигом в плоскости xоy.

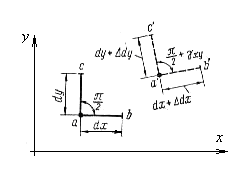
Рис. 7.6

Величины 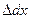и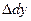имеют название абсолютных линейных деформацийв точке абруса в соответствующих направлениях, то есть в направлениях осей координат xи y.

Отношение абсолютной линейной деформации к начальной длине отрезка называется относительной линейной деформацией 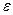, то есть:

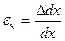и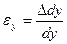

Мы рассмотрели деформации бруса в точке ав направлениях горизонтальных осей координат xи y. Но через точку абруса можно провести две вертикальные плоскости xоzиzоy. Тогда в направлении оси zможно определить абсолютную 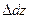и относительную 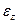линейные деформации в точке абруса:

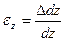
Углы между вертикальным отрезком 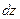и горизонтальными отрезкам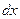и и 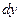также изменяются на величины 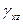и 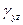соответственно.

Таким образом, деформации бруса в произвольной точке определяются при помощи трех независимых относительных линейных деформаций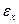; ; 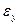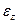,и трех относительных угловых деформаций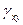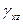й ; и .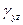

Совокупность шести приведенных выше деформаций определяют деформированное состояние бруса в произвольной его точке. Эти деформации имеют название составляющих тензора деформаций.

При деформации бруса каждая его точка перемещается в новое положение, а элементарные отрезки, которые имеют бесконечно малые длины, получают некоторые удлинения или укорочения, а также повороты относительно первоначального положения. Рассмотрим прямой брус (рис.7.7). До нагружения этот брус имеет прямолинейную ось и на рисунке он начерчен сплошными линиями. После нагружения брус деформируется и принимает криволинейную форму, начерченную на том же рисунке штриховыми линиями. Через произвольную точку А₁проведем некоторый бесконечно малый отрезок А₁А₂. После деформации бруса точка А₁переместится в положение А′₁, а отрезок А₁А₂переместится в положение А′₁А′₂и повернется относительно начального состояния на некоторый угол 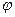. Величина 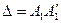на которую перемещается точка А₁в процессе деформации бруса называется линейным перемещением этой точки, а величина угла 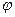на который повернется отрезок бруса в процессе деформации имеет название углового перемещения или угла поворота рассматриваемого отрезка. Вертикальная составляющая перемещения 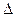обозначается буквой 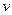и называется прогибом балки.

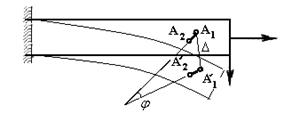
Рис.7.7