Бруса при растяжении и сжатии

Используем известные формулы.

Закон Гука σ = Еε.

Откуда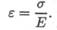

Относительное удлинение

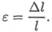
В результате получим зависимость между нагрузкой, размера­ми бруса и возникающей деформацией:

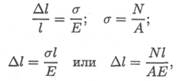
где Δ1 — абсолютное удлинение, мм;

σ— нормальное напряжение, МПа;

I — начальная длина, мм;

Е — модуль упругости материала, МПа;

N — продольная сила, Н;

А — площадь поперечного сечения, мм²;

Произведение АЕ называют жесткостью сечения.

Выводы

1. Абсолютное удлинение бруса прямо пропорционально вели­чине продольной силы в сечении, длине бруса и обратно пропорцио­нально площади поперечного сечения и модулю упругости.

2. Связь между продольной и поперечной деформациями зависит от свойств материала, связь определяется коэффициентом Пуассо­на, называемом коэффициентом поперечной деформации.

Коэффициент Пуассона: у стали μ от 0,25 до 0,3; у пробки μ = 0; у резины μ = 0,5.

3. Поперечные деформации меньше продольных и редко влияют
на работоспособность детали; при необходимости поперечная деформация рассчитывается через продольную.

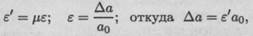
где Δа — поперечное сужение, мм; а0— начальный поперечный размер, мм.

3. Закон Гука выполняется в зоне упругих деформаций, которая
определяется при испытаниях на растяжение по диаграмме растя­жения (рис. 21.2).

При работе пластические де­формации не должны возникать, упругие деформации малы по сравнению с геометрическими размерами тела. Основные расче­ты в сопротивлении материалов проводятся в зоне упругих деформаций, где действует закон Гука.

На диаграмме (рис. 21.2) закон Гука действует от точки 0 до точки 1.

5. Определение деформации бруса под нагрузкой и сравнение ее с допускаемой (не нарушающей работоспособности бруса) называют расчетом на жесткость.