Зависимость теплового эффекта реакции от температуры

Приведенные ранее способы расчета тепловых эффектов применимы для определения DН при постоянной температуре (чаще всего стандартной, 298 К).

При температурах, отличных от стандартной, используют уравнение Кирхгофа.

В дифференциальном виде оно имеет вид,

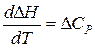(1.5)

где 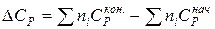есть разность между суммарными теплоемкостями продуктов реакции (конечных веществ) и исходных веществ (начальных).

Анализ уравнения (1.5):

1. Если DС_Р >0, то первая производная 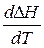> 0, следовательно функция DН растет с ростом температуры, то есть тепловой эффект возрастает, независимо от знака самого теплового эффекта (рисунок 1.2 а).

2. Если DС_Р < 0, то первая производная 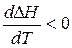, следовательно функция DН убывает с ростом температуры.

3. Если DС_Р= 0, то первая производная 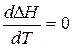. В этом случае DН = const, то есть не зависит от температуры. Если 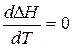при одной температуре, то при этой температуре будет экстремум (рисунок 1.2 б).

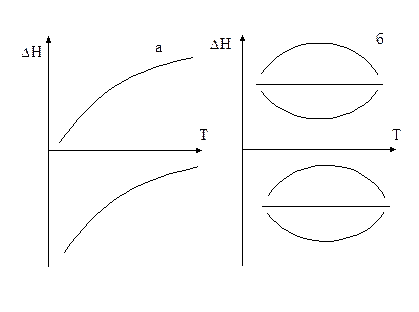
Рисунок 1.2 – Зависимость теплового эффекта от температуры

Интегрирование уравнения Кирхгофа приводит к уравнению, позволяющему рассчитать тепловой эффект реакции при любой температуре:

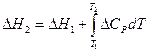(1.6)

где DН₂ - тепловой эффект реакции при любой температуре; DH₁ - тепловой эффект реакции при Т₁, рассчитанный одним из ранее приведенных способов.

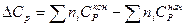
Расчет интеграла в уравнении 1.5 возможен с разной степенью точности:

1.

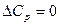
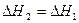
Это возможно в случае небольшого температурного интервала, а также в случае больших значений теплового эффекта, когда температурной зависимостью можно пренебречь.

2.

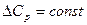
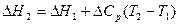
Если значение 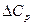в данном температурном интервале неизвестно, можно принять .

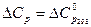3. 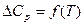. Обычно эта зависимость может быть получена из интерполяционных уравнений для С_р (1.4):

∆С_р = ∆а + ∆вТ +∆сТ² + ∆с^lТ ^-2 (1.7)

где 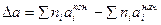; Δв, Δс, Δс^l находятся аналогично.

Подстановка уравнения 1.7 в уравнение 1.6 и интегрирование дает развернутое уравнение Кирхгофа:

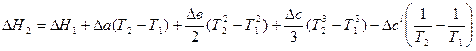(1.8)

Анализ температурной зависимости ΔН = f(T)

1.Исследование на экстремум.

Признаком существования экстремума является обращение в ноль первой производной исследуемой функции ΔН = f (T), т.е. 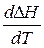по уравнению (1.8).

Из уравнения Кирхгофа:

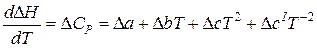(1.9)

Приравнивая к нулю полученное выражение, рассчитывается температура, при которой производная обращается в ноль. Приближенно можно ограничиться двумя слагаемыми в уравнении (1.9), т.е. .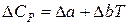

Если Т > 0 и ее значение лежит в интервале температур, в пределах которых действуют интерполяционные уравнения (интервалы указаны в справочнике), значит экстремум на кривой ΔН = f (T) существует. Для уточнения, какой именно экстремум (максимум или минимум) следует взять вторую производную и определить ее знак:

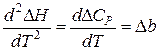
Если 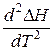> 0, то имеет место минимум, если 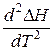< 0, то максимум.

Если же Т < 0 или лежит вне интервала температур, значит экстремум отсутствует и в исследовании функции переходим к пункту 2.

2.Для определения возрастающей или убывающей функции следует определить знак первой производной:

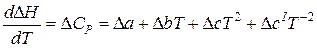
В это уравнение подставляется любая температура, взятая внутри интервала, и рассчитывается 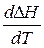: если 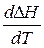> 0, то ΔН - возрастающая функция; если 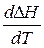< 0, то убывающая функция.

Для уточнения хода кривой определяют вторую производную и ее знак:

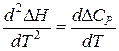> 0, то кривая вогнутая, при 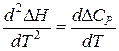<0 - выпуклая.