Математическое выражение

Второй закон термодинамики возник на основе изучения принципа действия тепловых машин, назначение которых состоит в превращении теплоты в работу. Основоположником является французский инженер С. Карно. Согласно Карно для периодического действия тепловой машины необходимо по меньшей мере два тепловых резервуара с различающимися температурами.

Если обозначить Q₁ – количество тепла, полученного системой (машиной) от нагревателя, а Q₂ – количество тепла, переданного системой более холодному телу (холодильнику), то Q₁ – Q₂ – количество тепла, превращенное в работу.

Отношение 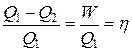является коэффициентом полезного действия.

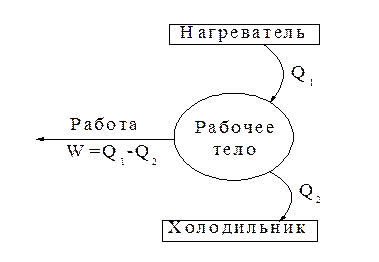
Рисунок 1.3 – Схема перехода тепла в работу

Рассмотрим идеальную машину, работающую по обратимому циклу Карно (две изотермы и две адиабаты) рисунок 1.4:

Рисунок 1.4 – Цикл Карно

Работа складывается из работ четырех процессов:

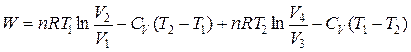
Запишем уравнения адиабат:

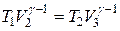
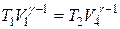
Разделив почленно левую и правую части первого уравнения на левую и правую части второго уравнения, получим: 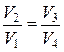, следовательно, в уравнении для W: 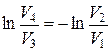, а .

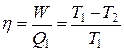Таким образом к.п.д. тепловой машины, работающей по обратимому циклу Карно, определяется лишь разностью температур нагревателя и холодильника и не зависит от рабочего тела этой машины.

Поскольку 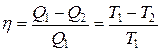, то можно записать 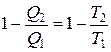или

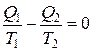
Это выражение может быть записано как 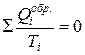и носит название теоремы Клаузиуса о приведенных теплотах:

«Алгебраическая сумма приведенных теплот обратимого цикла Карно равна нулю».

Если взять произвольный обратимый цикл и разбить на множество обратимых циклов Карно, получим: 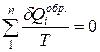, что в пределе дает при n→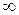

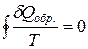
Из математики известно, что если круговой интеграл равен нулю, то подынтегральная функция является полным дифференциалом какой-то функции состояния:

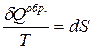(1.10)

Функция S называется энтропией.

Работа необратимого цикла меньше работы обратимого, т.е. 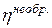< 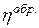, а значит 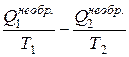< 0, или 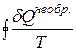< 0.

В этом выражении подынтегральная функция не является полным дифференциалом и

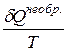< dS (1.11)

Объединив уравнения 1.10 и 1.11 получаем математическое выражение второго начала термодинамики:

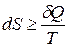или 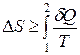(1.12)

Знак равенства относится к обратимому процессу, а знак больше к необратимому.

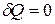
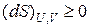Более простые соотношения получаются для изолированной системы, в которой:

или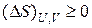

Заменяя δQ на выражение из первого начала термодинамики, получаем объединенное уравнение первого и второго начал термодинамики, так называемое фундаментальное уравнение термодинамики:

TdS 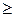dU + PdV + 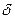W_X (1.13)