ЭДС индукции в движущихся проводниках

Используя определение магнитного поля (5л16) и сводя магнитную силу, действующую на проводник с током, к силам, испытываемым движущимися в нем зарядами, мы получили выражение для силы Лоренца (16л17). Согласно данному нами в лекции 15 определению, сила эта является сторонней (ибо она некулоновская) и должна возникать не только при движении зарядов внутри проводника (т. е. при наличии в нем тока), но и при любых перемещениях самого проводника в магнитном поле (так как при этом движутся и находящиеся в нем заряды). Следовательно, на различных участках такого проводника, вообще говоря, появляются сторонние электродвижущие силы, могущие вызывать электрический ток. Силы эти называются индукционными; для их расчета рассмотрим следующую простейшую схему.

Пусть прямолинейный отрезок цилиндрического проводника l перемещается в однородном магнитном поле B и пусть его скорость vперпендикулярна B и оси проводника (рис. 1). На положительные заряды q внутри будет, очевидно, действовать сила Лоренца, величина которой

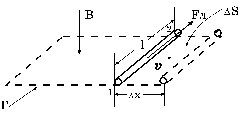Рис. 1.

F_л = qvB, (1)

а направление показано на рисунке. На отрицательные заряды сила F_л будет действовать в противоположном направлении. Возникающая на участке l ЭДС по определению

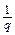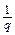e₁₂ = A₁₂ = F_лl = vBl (2)

и направлена[41] для зарядов обоих знаков вдоль изображенной на рис. 1 F_л.

Если представить себе, что отрезок l проводника является частью замкнутой квазилинейной цепи, контур которой изображен на рис. 1 пунктиром, то полученному результату может быть придана следующая форма. Поскольку ,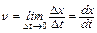

vBl = 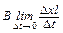= = 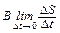= 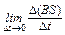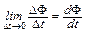, (3)

где DS = lDx – увеличение площади контура, а DФ = D(BS) – потока вектора B через него за время Dt. Так как остальные участки Г неподвижны, в них не появляются сторонние силы и, следовательно, полная ЭДС e, действующая вдоль всего контура, также определяется выражением (2). Из рис. 1 видно, что она составляет с направлением B левовинтовую систему. Таким образом, можно написать, что

e = 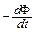, (4)

причем знак минус соответствует установленному нами в предыдущей лекции правилу, связывающему положительное направление обхода контура и положительную нормаль к нему посредством правого винта.

Можно показать, что соотношение (4) справедливо в самом общем случае произвольного движения (включая деформацию) контура в стационарном магнитном поле. Оно выражает собой так называемый закон индукции токов в движущихся проводниках: возникающая в контуре ЭДС индукции равна скорости изменения магнитного потока через контур и составляет с ним (т. е. с изменением) не право- (это означал бы знак «плюс» в (4)), а левовинтовую систему[42].

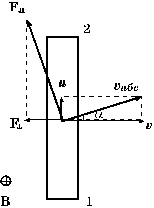Рис. 2.

Замечание 1. В законе индукции (4) речь идет о потоке вектора B через замкнутый контур Г, хотя имеется в виду, конечно, поток его через какую-либо поверхность, опирающуюся на этот контур (ведь именно через поверхность и определяется поток любого вектора). Нетрудно видеть, что произвол в выборе этой поверхности не скажется на величине Ф. Действительно, натягивая на контур Г две произвольные поверхности S₁ и S₂, мы получим замкнутую поверхность S_S , поток вектора B через которую согласно уравнению (9л17) равен нулю. Это значит, что потоки через S₁ и S₂ равны и противоположны, причем по смыслу (9л17) нормали к S₁ и S₂ при этом должны быть направлены наружу, т. е. одна из них образуют с направлением обхода Г правовинтовую, а другая – левовинтовую системы. Меняя направление последней на противоположное (а вместе с ней и знак соответствующего Ф), получаем независимость потока, входящего в (4), от выбора поверхности S[43].

Замечание 2. При выводе формулы (2) предполагалось, что движущийся в магнитном поле отрезок проводника замкнутой цепи не образует, т. е. в нем ток не течет, хотя полученный в результате ее обобщения закон (4) относится именно к замкнутому проводящему контуру. Посмотрим, к каким эффектам приведет появление тока в рассматриваемом проводнике (рис. 2). Возникновение скорости u упорядоченного движения носителей, направленной вдоль оси проводника, вызовет поворот на некоторый угол a абсолютной скорости v_абс зарядов относительно направления движения проводника (т. е. v). При этом сила Лоренца F_л оставаясь всегда перпендикулярной v_абс , тоже повернется на угол a относительно оси проводника. Однако величина продольной ее составляющей, создающей ЭДС e₁₂ ,

F_|| = F_л cos a = qv_абс B cos a = qBv

по-прежнему будет определяться формулой (1), так что выражения (2) – (4) останутся справедливыми. Поперечная же составляющая, равная по величине

F_^ = F_л sin a = qv_абс B sin a = qBu,

очевидно, представляет собой силу, направленную навстречу движению проводника[44]. На преодоление этой силы (просуммированной по всем движущимся зарядам внутри объема данного проводника) и затрачивается внешняя работа, необходимая для его перемещения в магнитном поле.

Обратив порядок рассуждений, приведенных в предыдущей лекции при выводе соотношения (15л17), получим для этой суммарной силы F_^S известное выражение (5л16), откуда развиваемая ей механическая мощность

P¢_мех = – F_^Sv = – IBlv.

Мощность же сторонних сил, определяемых продольной составляющей F_|| , на участке 1–2 проводника в соответствии с (2)

P_стр = e₁₂I = vBlI

и оказывается равной – P¢_мех . Таким образом,

P¢_мех + P_стр = 0,

т. е. полная работа сил магнитного поля (как уже отмечалось ранее) равна нулю. Для поддержания движения проводника внешняя сила, уравновешивающая F_^S , должна, очевидно, развить мощность

P_мех = – P¢_мех = P_стр ,

которая и «перейдет» в работу (в единицу времени) действующих внутри него сторонних сил индукции[45].

Аналогичные явления происходят и при движении в магнитном поле проводника, к концам которого приложена разность потенциалов. Если проводник неподвижен, то ток на участке 1 – 2 (рис. 3) течет только за счет электрических сил. Если же его «отпустить», то под действием магнитной силы появится скорость v и абсолютная скорость носителей v_абс отклонится от оси проводника. Тотчас же повернется и сила F_л Лоренца и возникнет ее осевая составляющая F_|| , направленная навстречу току. Она повлечет за собой появление сторонней ЭДС e₂₁ для компенсации действия которой (т. е. сохранения неизменным тока) источнику необходимо развить дополнительную мощность e₂₁I. Повторяя приведенные выше рассуждения, нетрудно показать, что именно эта мощность «выделится» в виде совершенной проводником (в единицу времени) механической работы. Таким образом, и в этом случае полная работа силы Лоренца, конечно, оказывается равной нулю (ибо F_л ^ v_абс). Отрицательная часть ее, вызванная F_|| , компенсируется работой источника тока, положительная же представляет собой полезную работу проводника.

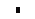Рис. 3.