Энергия магнитного поля

Поскольку возникающая ЭДС самоиндукции и, следовательно, собственная энергия тока обусловлены появлением меняющегося магнитного поля, естественно попытаться связать эту энергию именно с полем. Для этого выразим собственную энергию тока в соленоиде через индукцию возбуждаемого им однородного поля. С учетом (8) и (12л17)

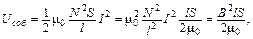
т. е. энергия эта оказывается пропорциональной объему V = lS, занятому полем. Ее называют энергией магнитного поля W_m , а энергию, приходящуюся на единичный объем

w_m = 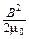(13)

– плотностью энергии поля.

Можно показать, что в общем случае неоднородного поля произвольной системы токов их полная энергия, т. е. работа, которую нужно затратить против сил индукции, чтобы возбудить эти токи, представима в виде энергии магнитного поля

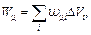(14)

где суммирование распространяется на весь объем, занятый полем.

В рамках магнитостатики оба взгляда на энергию равноправны, ибо одинаково хорошо согласуются с экспериментом. Изучая же переменные электромагнитные поля, мы увидим, что там эквивалентность этих трактовок нарушается и опыту соответствует лишь представление о локализации энергии в электромагнитном поле[53].

[1] Очевидно, приводимые рассуждения не зависят от знака свободных носителей заряда. Если ими являются отрицательные частицы, то нужно все направления движения зарядов на рис.1 заменить на обратные.

[2] Поскольку скорость движения свободных зарядов в проводниках, как показывает опыт, под действием электрического поля не возрастает до «бесконечности», мы обязаны предположить, что в них имеются некие силы, тормозящие это движение. Поэтому между интенсивностью движения зарядов и электрическим полем должна быть какая-то связь.

[3] Строго говоря, мы должны постулировать это утверждение.

[4] Очевидно, что через любое сечение проводника протекает один и тот же ток (если этот проводник не имеет разветвлений), иначе в определенных его участках происходило бы накапливание заряда, электрическое поле менялось бы и ток не был бы постоянным.

[5] Он может зависеть также от внешних условий, в частности, от температуры.

[6] Речь идет, конечно, об усредненном по большому числу этих носителей направлении их движения. При таком усреднении тепловые скорости частиц, взаимно уничтожаясь, вклада в это направление не дадут и оно целиком будет определяться лишь средней, «дрейфовой», скоростью их упорядоченного движения как целого.

[7] При установлении тока такие процессы возможны, однако поперечный ток будет длиться до тех пор, пока накапливающийся на поверхности заряд, создавая собственное поле, не обратит в нуль поперечное поле в любой точке проводника (как в электростатике!).

[8] См. сноску ⁵ на стр. 5.

[9] Доказательство основывается на линейности полной системы уравнений электростатики (7л11) и теореме единственности (см. сноску ⁵⁰ на стр. 62).

[10] Мы не рассматриваем точек неопределенности поля, где E = 0 (ср. сказанное о силовых линиях в лекции 11).

[11] Фактически мы уже использовали понятие квазилинейного тока в § 9.4, когда рассчитывали сопротивление проводника произвольной формы.

[12] Действующую на каком-либо участке цепи ЭДС принято изображать знаком 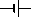. При этом поле сторонних сил считается направленным от короткого перпендикулярного отрезка к длинному (т. е. на данном рисунке слева направо).

[13] Строго говоря, это справедливо лишь в том случае, когда природа сторонних сил такова, что не предполагает превращения теплоты, заимствованной от окружающих тел (или самого проводника) в их работу. Такое, однако, выполняется не всегда. Например, при контакте двух различных металлов в зависимости от направления проходящего через контакт тока в нем может выделяться или поглощаться так называемое тепло Пельтье, связанное как раз с особой природой действующих в контакте сторонних сил. Соотношение (14) будет, разумеется, справедливо и в этом случае (ибо в нем природа сторонних сил несущественна), но член 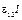, представляющий собой мощность сторонних сил, фактически даст выделившееся или поглотившееся тепло, которое надо добавить (с соответствующим знаком) к джоулеву. Мы, впрочем, такие ситуации рассматривать не будем.

[14] Очевидно, что в этом случае 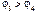, ибо ток может течь навстречу сторонним силам лишь при наличии превосходящих и противоположно направленных электрических сил.

[15] Такие токи с бесконечно малым поперечным сечением мы будем называть линейными.

[16] Ситуация здесь оказывается сложнее, чем в электростатике, ибо элемент тока, в отличие от элемента заряда, является вектором, т. е. не изотропен (имеет выделенное направление).

[17] Это определение В справедливо в системе единиц СИ. В других системах оно может отличаться от (5) присутствием постоянного размерного коэффициента.

[18] На первый взгляд кажется, что приведенное определение В является чересчур сложным и неоправданно громоздким. Более наглядным и простым может представиться введение В, скажем, через максимальный момент сил, действующих на маленькую рамку с током, как это сделано, например, в школьном учебнике физики. Однако такой путь логически не вполне корректен. Дело в том, что определяя В как некий материальный объект, агент, ориентирующий рамку, мы не сможем ответить на вопрос, как этот агент будет действовать на произвольный контур с током, или какую-либо его часть, ибо произвольный участок цепи нельзя составить из отдельных рамок. Главным свойством В, которое должно быть положено в основу его количественного определения, должна служить способность магнитного поля воздействовать именно на малый участок тока, т. е. на универсальный элемент, из которого может быть составлен любой ток. Другая причина несостоятельности подобного подхода заключается в том, что воздействие поля на рамку с током в общем случае не исчерпывается ориентирующим эффектом, и даже в тех случаях, когда исследуемую цепь можно представить совокупностью рамок с током, расчет влияния на нее магнитного поля путем только суммирования вращающих моментов, дает просто неверный результат (ибо не учитывает действующих на рамку деформирующих усилий).

[19] Существуют и другие модификации этого правила.

[20] Часто его называют законом Био – Савара – Лапласа.

[21] Необходимость введения в формулу (8) этого коэффициента связана с тем обстоятельством, что единицы всех входящих в нее величин уже выбраны. Как выяснится в дальнейшем, единица m₀ связана с единицей индуктивности – генри (Гн): m₀ измеряется в Гн/м (ср. с единицей измерения e₀).

[22] См. по этому поводу также третью сноску к § 8.3.

[23] В этом случае поле является электромагнитным и не статическим, ибо мы рассматриваем два изолированных элемента тока (не входящие в замкнутые цепи), которые создают вокруг себя меняющиеся со временем электрическое и магнитное поля. Такое поле обладает определенным тоже меняющимся импульсом, задаваемым значениями Е и В в каждой точке.

[24] В случае электрического поля циркуляция вектора Е, как мы видели, представляет собой работу электрических сил вдоль замкнутого контура, отнесенную к величине заряда. В магнитном поле такого ясного физического содержания циркуляция не имеет.

[25] С точностью до знака.

[26] Случай, когда контур Г охватывает ток несколько раз, физического интереса не представляет и нами рассматриваться не будет (хотя он без труда рассчитывается).

[27] Наличие замкнутых петель на контуре Г, не охватывающих ток (см. рис. 3), очевидно, не влияет на результат, поскольку циркуляцияВ по каждой такой петле равна нулю.

[28] В том числе и тогда, когда контур Г находится внутри проводящей среды, по которой течет непрерывно распределенный постоянный ток. Такие случаи, однако, мы в настоящей лекции не рассматриваем.

[29] Часто второе утверждение включает и первое, т. е. под полнотой понимают и единственность.

[30] В такой формулировке эта теорема не вполне аналогична теореме единственности в электростатике (см. лекцию 11), ибо там задавалось не распределение заряда σ, а потенциалы (или заряды) проводников, на которых устанавливалось какое-то σ, и доказывалась единственность не только образованного им поля, но и самого этого распределения, т. е. рассматривалась более сложная задача.

[31] Ср. все сказанное по этому поводу об электростатическом поле в лекции 11.

[32] Разумеется, при условии (которое мы считаем выполненным), что линии эти проводятся так, чтобы густота их была пропорциональна B. Тогда (как мы видели в лекции 11) число линий, пересекающих какую-либо поверхность, пропорционально потоку соответствующего вектора через эту поверхность.

[33] Существует еще одна возможность: линия В, непрерывно извиваясь, может бесконечно продолжаться, оставаясь все время внутри некоторого ограниченного объема. Поскольку линия эта «толщины» не имеет, она никогда не заполнит этот объем и нигде не оборвется. Такие линии не противоречат системе (10 В) и, в отличие от электрических, действительно существуют (ср. со сказанным о линиях Е в последней сноске к § 8.11). Подобные ситуации, однако, мы рассматривать не будем как редко встречающиеся и не представляющие практического интереса.

[34] Соображения симметрии с равным правом, очевидно, применимы к пространствам как внутри, так и снаружи соленоида.

[35] Утверждение о стремлении к нулю поля бесконечного соленоида при удалении от него нуждается в более убедительной аргументации, поскольку число его витков бесконечно велико. Понятно, что основной вклад в поле в любой точке М, расположенной снаружи соленоида, будет давать его отрезок конечной длины, видный из этой точки под близком к π углом 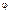. Если этот угол разбить на малые части Δφ_i, то при удалении точки М от соленоида и фиксированных Δφ_i внутрь каждого из них будет попадать все большее число витков, создающих в М неизменное по направлению поле ΔB_i (сохраняется подобие). Поскольку, однако, ΔN растет пропорционально расстоянию r точки М от соленоида, а поле каждого витка по величине спадает не медленнее, чем 1/r², вклад в поле i-го участка соленоида, соответствующего углу Δφ_i, будет уменьшаться, причем не медленнее, чем 1/r. Стало быть, не медленнее, чем 1/r, будет спадать и суммарное поле всех таких участков (ср. вышесказанное с рассуждениями, приводимыми в § 8.5 при обсуждении электрического поля бесконечной заряженной плоскости. Ситуации здесь и там оказываются разными, ибо соленоид – система, бесконечная в одном измерении, а плоскость – в двух).

[36] Через перпендикулярную скорости u площадку DS за время Dt пройдут все частицы, находящиеся внутри цилиндра с основанием DS и высотой uDt. Они перенесут заряд DQ = qnDSuDt откуда для плотности тока j = 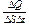получается выражение (14).

[37] Часто силой Лоренца называют полную силу, испытываемую движущимся зарядом со стороны магнитного и электрического полей, т. е. прибавляют к правой части (16) еще силу qE. Мы сохраним это название лишь за ее магнитной частью.

[38] Это обстоятельство не противоречит принципу действия электродвигателя, где движение проводника с током в магнитном поле сопровождается совершением механической работы. Такое движение не эквивалентно перемещению свободных зарядов, и на него накладываются возникающие здесь явления электромагнитной индукции (см. следующую лекцию).

[39] При условии, конечно, что v << c и m = const.

[40] Аналогичное явление, вызванное изменением электрического поля, будет рассмотрено позже, в разделе «Электромагнитные волны».

[41] ЭДС есть скаляр (работа, деленная на заряд) и направления не имеет. Здесь имеется в виду направление оси, вдоль которой ЭДС положительна. В дальнейшем мы иногда будем применять подобные нестрогие выражения, ибо они вполне понятны и отличаются лаконичностью.

[42] Точнее, левовинтовую систему ЭДС должна составлять с направлением нормали (ведь Ф и dФ – тоже скаляры !), проведенной таким образом, чтобы dФ было положительным (см. предыдущую сноску).

[43] Сp. Подобные рассуждения, приведенные в предыдущей лекции при обсуждении теоремы о циркуляции. Аналогия здесь полная, ибо как линии j, так и линии В не имеют истоков.

[44] Рассмотрение на рис. 2 проводится для положительных свободных зарядов. В случае отрицательного их знака (и том же токе) на противоположные изменятся лишь направления uи F_|| ; направление же F_^ останется прежним.

[45] Описанные процессы лежат в основе работы генератора – машины, преобразующей механическую работу в работу индуцируемых в ее обмотке электродвижущих сил.

[46] Различия эти имеют глубокие физические причины и связаны с релятивистским преобразованием длин и времен и инвариантностью заряда.

[47] Причины эти могут действовать одновременно, т. е. контур может перемещаться и деформироваться, а магнитное поле при этом меняться в каждой точке.

[48] См. сноску ⁴⁰ на стр.52.

[49] Мы ввели эту единицу раньше, используя выражение (6л16) для величины магнитной индукции. Поскольку коэффициенты в определении магнитного поля (5л16) и законе электромагнитной индукции (4) одинаковые (во всех системах единиц), определения эти вполне эквивалентны друг другу.

[50] Доказательство основывается на очевидной линейности электростатической и магнитостатической систем уравнений (10л17 А и В) и соответствующих теоремах единственности. Линейность означает, что сумма любых двух решений этих уравнений тоже является их решением. Если два распределения зарядов (создающих электрическое поле и ток в проводнике) и токов наложить друг на друга, то поля тоже наложатся, и если каждая система зарядов, токов и полей порознь удовлетворяла всюду уравнениям (10л17), то будет удовлетворять им и их сумма. Если эти решения одинаковые, то это и значит, что «все» удвоится, причем в силу теорем единственности указанная ситуация оказывается единственно возможной.

[51] Это обстоятельство нисколько не сужает границ применимости понятия индуктивности: ведь бесконечно тонкий проводник подразумевает бесконечную плотность тока, что физически бессмысленно. При переходе же к непрерывно распределенным токам поле получается всюду конечным и подобных «неприятностей» с Ф_соб ® ¥ не возникает.

[52] Это – так называемые экстратоки размыкания, вредное явление, для борьбы с которым применяют специальные меры. На этом же принципе основана работа индукционных катушек, служащих для получения высоких импульсных напряжений.

[53] Ср. сказанное в лекции 13 об энергии электростатического поля.