Вектор магнитной индукции

Как показывает опыт, сила F, испытываемая малым элементом линейного тока со стороны других токов, или, что то же самое, со стороны создаваемого ими поля, пропорциональна произведению величины тока I на длину элемента Dl. Поэтому отношение этой силы к произведению IDl уже не зависит от параметров рассматриваемого элемента тока и может служить количественной характеристикой внешнего поля, в которое помещен этот элемент. Однако все тот же опыт показывает, что действие данного поля на элемент зависит еще и от его ориентации, так что простое деление F на IDl поля не даст[16]. Из трех векторов F, Dl и поля нужно сконструировать, если это возможно, такую комбинацию, чтобы изменение ориентации Dl, приводящее к изменению F, не меняло величины и направления внешнего магнитного поля, действующего на данный элемент (иначе это поле уже не будет внешним, не зависящим от манипуляций с нашим элементом). Эксперимент говорит, что это возможно, и дает следующее соотношение, которое следует рассматривать как определение магнитного поля[17]:

F = I [Dl, B], (5)

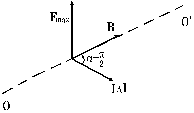Рис. 2.

где B – вектор магнитной индукции (называемый так по исторически сложившейся терминологии), вполне аналогичный вектору электрического поля E, а Dl направлен, очевидно, в ту сторону, куда течет ток в рассматриваемом элементе. Вектор B мы часто будем называть вектором магнитного поля или просто магнитным полем.

Таким образом, чтобы экспериментально определить магнитное поле в какой-либо точке пространства, нужно поместить в эту точку малый элемент тока IDl (рис. 2) и, изменяя его ориентацию, добиться такого положения (а их, как показывает опыт, если B ¹ 0, всегда только два), при котором действующая на него сила обратится в нуль. Вектор B, очевидно, будет в этом случае параллелен или антипараллелен элементу (пунктир OO¢ на рис. 2), ибо sin a = 0 и F ~ sin a = 0. Повернув далее Dl в произвольной плоскости на p / 2 относительно OO¢ и измерив силу 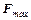, испытываемую элементом, найдем магнитное поле по величине и направлению:

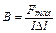, (6)

а направлено оно так вдоль OO¢, чтобы векторы Dl, B и 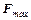образовывали правовинтовую тройку[18].

Наоборот, зная вектор B в любой точке пространства, можно сразу по формуле (5) найти силу, действующую на малый элемент тока. По величине

F = IDlB sin a, (7)

а направление ее всегда перпендикулярно току и определяется правилом правого винта. Часто правило, устанавливающее взаимную ориентацию векторов, образующих векторное произведение, формулируют, ссылаясь не на винт с правой резьбой или стрелку часов, а на левую руку человека[19]. Тогда его называют правилом левой руки, и для нашего случая оно звучит следующим образом: если левую руку расположить так, чтобы вектор B «входил» в ладонь, а четыре пальца «смотрели» вдоль тока, то отогнутый большой палец укажет направление действующей на элемент силы.

Из (6) может быть получена единица индукции магнитного поля в системе СИ. Она имеет специальное название – тесла (Тл). Очевидно,

1 Тл = 1 .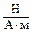

Во всех приведенных рассуждениях фигурировал малый элемент, «кусочек» постоянного тока, который, как известно, сам по себе, отдельно, существовать не может. Ведь любая цепь постоянного тока обязана быть замкнутой (или идти из бесконечности в бесконечность), а потому рядом с выделенным ее элементом всегда находятся другие. Можно ли в таком случае говорить о силе, действующей на отдельный элемент, и если да, то как ее измерить?

Рис. 3.

Несмотря на замкнутость постоянных токов, говорить о такой силе можно. Для ее экспериментального определения достаточно закрепить все участки цепи, предназначенной для исследования магнитного поля, оставив подвижным лишь малый ее отрезок (например так, как изображено на рис. 3, где короткая перемычка Dl может скользить по двум направляющим, оставаясь с ними в контакте), и измерить силу, действующую на этот отрезок (хотя бы по силе, которую нужно приложить к нему, чтобы удержать его в равновесии). Ориентируя различным образом весь этот контур и измеряя всякий раз силу, испытываемую его подвижным элементом, можно по описанному рецепту найти B в любой точке. При этом, конечно, «пробный» элемент тока IDl должен удовлетворять определенным требованиям, аналогичным тем, которым удовлетворяет пробный заряд в электростатике. Элемент этот обязан быть достаточно малым по размеру, так чтобы исследуемое поле на всем его протяжении было постоянным в пределах заданной точности, и величине тока I, чтобы действие этого элемента (а точнее, всей цепи, в которую он входит) на токи, создающие данное поле, не приводило к заметному перераспределению их в пространстве и не искажало, таким образом, исследуемого поля. Кроме того, ток I, текущий по измерительной цепи, должен быть настолько малым, чтобы остальные ее участки не оказывали существенного влияния на ее подвижный элемент. Другими словами, собственное поле контура в месте расположения 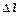должно быть много меньше внешнего. В дальнейшем мы будем считать все эти условия выполненными.