Полная система уравнений магнитостатики. Теорема единственности

Теорема о циркуляции является одним из основных уравнений магнитостатики. Для образования полной системы к ней нужно добавить еще одно уравнение, которое ввиду сложности его вывода мы приводим без доказательства. Оно утверждает, что поток вектора B через любую замкнутую поверхность S всегда равен нулю:

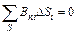. (9)

Можно показать, что система уравнений (8) и (9) полностью эквивалентна закону Био – Савара и принципу суперпозиции, т. е. из одной пары этих утверждений следует другая, и наоборот. Отсюда вытекает, что, во-первых, уравнения (8) и (9) составляют полную систему уравнений магнитостатики, т. е. всякое магнитное поле постоянных токов обязано им удовлетворять и, наоборот, любое поле, удовлетворяющее этим уравнениям во всем пространстве, является магнитостатическим, т. е. может быть создано каким-то образом распределенными постоянными токами. Во-вторых, справедлива следующая теорема единственности[29]: если известно распределение токов, то однозначно определятся возбуждаемое ими магнитное поле B, и обратно, задание B влечет за собой единственно возможное распределение токов[30]. Действительно, процедура вычисления поля данных токов по закону Био – Савара и принципу суперпозиции однозначна, причем поле это в силу отмеченной эквивалентности утверждений удовлетворяет уравнениям (8) и (9). С другой стороны, если заданное поле везде удовлетворяет этим уравнениям, то, используя лишь первое из них, можно найти распределение токов, создающих его (ведь по (8) для знания тока, текущего через произвольную маленькую петельку Г, достаточно найти циркуляцию вдоль нее вектора B). Поскольку и эта операция является однозначной, отсюда следует единственность распределения токов.

Итак, для анализа стационарного магнитного поля можно пользоваться либо законом Био – Савара и принципом суперпозиции, либо полной системой уравнений (8) и (9). Последняя может оказаться весьма полезной в случаях особой симметрии распределения токов, позволяя сразу найти поле B, минуя громоздкие вычисления с привлечением закона 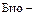Савара. Кроме того, если решение задачи угадано из других соображений, она дает возможность проверить его верность и утверждать единственность. Наконец – и в этом главная ее ценность, – система эта может быть преобразована к дифференциальной форме, в которую входят характеристики, относящиеся к одной и той же точке пространства. Эта форма является незаменимой для теоретического исследования магнитных полей[31].

Сейчас мы используем эту систему для сравнительного анализа магнитного и электрического статических полей. Выпишем основные уравнения электро- и магнитостатики

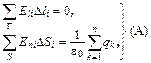
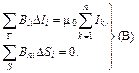(10)

справедливые соответственно для любого замкнутого контура Г и любой замкнутой поверхности S. Общим между этими уравнениями является то, что в левые их части входят одинаковые комбинации – циркуляция вектора вдоль кривой и поток его через поверхность. Значит, и электрическое, и магнитное поля «устроены» таким образом, что однозначно определяются заданием этих комбинаций в любой области пространства, причем последние связаны лишь с распределением зарядов или токов. Там, где нет ни тех, ни других, уравнения для E и B становятся одинаковыми, а значит, поля эти совпадают по всем своим свойствам.

Однако в областях, занятых зарядами или токами, поля оказываются существенно различными, и различия эти определяются разницей правых частей уравнений систем (А) и (В). Из первого уравнения (В) следует, что магнитное поле, в отличие от электрического, является полем непотенциальным: в нем существуют контуры (охватывающие токи), циркуляция по которым не равна нулю. Отсюда вытекает принципиальная возможность существования замкнутых линий индукции, которая для линий E запрещалась первым уравнением (А) (такие линии, например, имеет поле прямого тока). Но может быть, наряду с замкнутыми линиями B существуют и незамкнутые, обрывающиеся в каких-то точках пространства (например там, где текут токи)? Первому уравнению (В) такая возможность не противоречит. Однако второе уравнение (В) утверждает, что таких линий не существует. Линии индукции не имеют истоков, т. е. точек, где они могли бы начинаться или кончаться[32]. Ведь в противном случае, окружая такую точку замкнутой поверхностью, мы пришли бы к нарушению второго уравнения (В), ибо число входящих в эту поверхность линий не равнялось бы числу выходящих и поток через нее был бы отличен от нуля. Стало быть, линии индукции магнитного поля могут быть либо замкнутыми, либо двумя концами уходить в бесконечность[33]. Такие поля называются вихревыми в противоположность потенциальным, представителем которых является электростатическое поле.

Пример. В качестве иллюстрации применения основных уравнений (10 В) найдем поле «бесконечного» соленоида. Под «бесконечным» соленоидом понимается длинный круговой цилиндр, на поверхности которого намотан по винтовой линии с малым шагом проводник. Если длина цилиндра много больше его диаметра, который, в свою очередь, намного превосходит шаг винтовой линии, то систему можно считать однородной вдоль оси цилиндра (пока мы находимся далеко от его концов), а виток провода – перпендикулярной этой оси окружностью, т. е. система оказывается еще и аксиально-симметричной (рис. 10). Отсюда следует, что каждая из трех составляющих 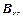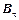и 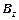поля может зависеть лишь от одной координаты – расстояния r от оси соленоида.

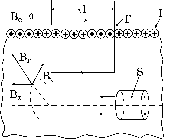Рис. 10.

Покажем сначала, что поле внутри не имеет радиальных составляющих B_r . Для этого построим «гауссову» поверхность – коаксиальный цилиндр, расположенный внутри или вне[34] соленоида. Из однородности системы вдоль оси следует, что суммарный поток B через его донышки равен нулю (входящий через одно донышко равен выходящему через другое). Из аксиальной же симметрии задачи вытекает, что вектор B_r всюду на боковой поверхности направлен наружу или внутрь, а потому поток через нее может быть равным нулю лишь при условии B_r = 0.

Далее, B_t = 0 по теореме о циркуляции. Выбирая перпендикулярную оси цилиндра окружность с центром на его оси и используя аксиальную симметрию задачи, нетрудно видеть, что циркуляция B вдоль этой окружности, не имеющей сцепленных с ней токов, равна нулю лишь при условии B_t = 0.

Для определения B_z проведем плоский замкнутый прямоугольный контур Г, стороны которого попарно параллельны и перпендикулярны оси цилиндра и пересекают обмотку соленоида. Найдем циркуляцию B вдоль этого контура, связав положительное направление его обхода с направлением тока I правилом правого винта. Учитывая, что вертикальные стороны Г вклада в циркуляцию не дают (ибо 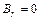), получим

,

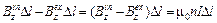где 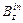и 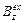– z-проекции поля соответственно внутри и снаружи соленоида на горизонтальных участках Г, n – число витков на единицу его длины, а 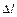– длина продольной стороны контура. Отсюда разность

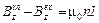(11)

и не зависит от высоты прямоугольника Г. Устремляя эту высоту к бесконечности, получим, что поле 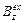сохраняет какое-то постоянное значение при удалении от соленоида на сколь угодно большие расстояния. Но представляя это поле как суперпозицию полей отдельных витков, нетрудно видеть, что оно должно убывать при удалении от соленоида, ибо поле каждого витка согласно закону Био – Савара спадает с расстоянием r до него не медленнее, чем 1/r² (расчеты показывают даже, что при больших r оно ~1/r³). Следовательно, постоянное значение 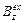может быть только нулевым, т. е. поле снаружи соленоида везде равно нулю. Отсюда из (11) сразу получаем

.

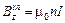Таким образом, поле внутри соленоида однородно, направлено вдоль оси, составляет с направлением тока правовинтовую систему и по величине

B = m₀nI, (12)

а снаружи равно нулю[35].

Сила Лоренца

Выражение (5л16) для силы, испытываемой проводником с током в магнитном поле, положенное в основу определения B, может быть преобразовано к виду, позволяющему понять механизм ее появления. Для этого рассмотрим отрезок цилиндрического проводника длины Dl и сечения S с квазилинейным током I и напишем цепочку очевидных равенств

F = I [Dl, B] = [IDl, B] = [ jSDl, B] = SDl [ j, B], (13)

где j – плотность тока, параллельная, очевидно, Dl(из определения векторного произведения следует, что скаляр можно вносить под его знак и выносить оттуда). Но плотность тока j выражается через концентрацию носителей n, их заряд q и среднюю скорость упорядоченного движения u:

j = qnu[36], (14)

что после подстановки в (13) дает

F = SDlqn[u, B] = Nq[u, B], (15)

где N – число движущихся частиц в объеме проводника SDl. Таким образом, сила F, испытываемая отрезком проводника с током, оказывается пропорциональной числу движущихся в нем зарядов. Совершенно естественно предположить, что она приложена именно к этим движущимся зарядам, равномерно распределяясь между ними. За счет столкновений их с неподвижными ионами она «передается» последним и с макроскопической точки зрения воспринимается как сила, действующая на весь проводник. Из сделанного предположения следует, что на каждый движущийся заряд действует сила

F_л = q[v, B], (16)

где v – истинная скорость заряда (включая и тепловую): ведь тепловые скорости благодаря своей хаотичности вклада в (15) все равно не дадут.

Опыты, проведенные со свободно движущимися зарядами (например с электронными или ионными пучками), позволяющие непосредственно определить испытываемую ими силу, подтверждают верность формулы (16), причем она остается справедливой не только в постоянном, но и в переменном магнитных полях. Сила, определяемая выражением (16), называется силой Лоренца[37].

Как видно из (16), сила Лоренца перпендикулярна скорости заряда (и индукции магнитного поля), а потому работа ее над движущейся частицей всегда равна нулю. Таким образом, магнитное поле не может разогнать или затормозить эту частицу, а способно лишь искривить ее траекторию[38].

Пример. Электрон «встреливается» в однородное магнитное поле B перпендикулярно линиям индукции. Описать его движение.

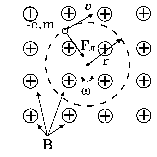Рис. 11.

Так как начальная скорость электрона v ^ B, то движение его будет происходить в перпендикулярной полю плоскости (рис. 11). Действительно, сила Лоренца всегда перпендикулярна полю, а потому продольная ее составляющая равна нулю. Не может появиться, следовательно, и продольная составляющая скорости. Далее, так как в магнитном поле всегда v = const и v ^ B,то F_л = qvB = const.

Таким образом, электрон будет двигаться с постоянной по модулю скоростью под действием постоянной по величине силы, перпендикулярной скорости. Это – движение по окружности. Записывая второй закон Ньютона для этого движения, получим

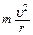= evB,

или

mw²r = ewrB,

где r – радиус окружности, а w – угловая скорость (круговая, или так называемая циклотронная, частота вращения). Из второго соотношения следует, что циклотронная частота вращения электрона

w =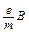

определяется лишь величиной магнитного поля и не зависит от скорости электрона[39]. Из первого равенства радиус вращения

r =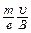

и увеличивается с ростом v. Отметим, что на постоянстве циклотронной частоты основана работа одного из типов ускорителей частиц – циклотрона.

Контрольные вопросы и задания

1. Найти поле прямого бесконечного тока.

2. Дать определение ампера.

3. Что такое циркуляция вектора вдоль какой-либо замкнутой кривой? Это вектор или скаляр? Арифметическая или алгебраическая величина?

4. Найти циркуляцию вектора В, созданного прямым бесконечным током, вдоль замкнутого контура, лежащего в перпендикулярной току плоскости.

5. Показать, что циркуляция поля прямого тока вдоль произвольной кривой равна циркуляции вдоль проекции этой кривой на перпендикулярную току плоскость.

6. Сформулировать теорему о циркуляции. Как определяются знаки фигурирующих в ней токов?

7. Показать, что сумма постоянных токов, пронизывающих поверхность, опирающуюся на какой-либо замкнутый контур, не зависит от формы этой поверхности.

8. Написать полную систему уравнений магнитостатики. Что означает её полнота? Каким двум фундаментальным утверждениям она полностью эквивалентна?

9. Сформулировать магнитостатическую теорему единственности. Сравнить её с электростатической аналогичной теоремой.

10. Доказать, что магнитные линии не имеют истоков.

11. Сравнить кулоновское и магнитостатическое поля в областях пространства, свободных от зарядов и токов.

12. То же для областей, занятых (не целиком) зарядами и токами.

13. Показать, что магнитное поле длинного соленоида не имеет радиальных и «круговых» составляющих.

14. Найти поле соленоида внутри и снаружи.

15. Исходя из определения магнитного поля, получить выражение для силы Лоренца. Показать, что сила Лоренца не может разогнать или затормозить частицу.

16. Описать движение электрона, который «встреливается» в однородное магнитное поле перпендикулярно его линиям.

Лекция 18

Глава 11. Электромагнитная индукция

До сих пор мы рассматривали статические, т. е. не меняющиеся во времени электрические и магнитные поля. Они создавались соответственно неподвижными зарядами и постоянными токами. А что произойдет, если заряды начнут двигаться, а токи меняться? Естественно считать, что если изменения и перемещения эти происходят достаточно плавно, то поля останутся статическими, соответствующими распределению зарядов и токов в данный момент времени, и будут медленно меняться вместе с ними. Фактически мы уже сталкивались с подобной ситуацией, когда считали, например, взаимную энергию зарядов и рассматривали работу кулоновых сил при их удалении друг от друга на бесконечность (см. лекцию 12).

Однако при таких изменениях положений или величин зарядов и токов и возбуждаемых ими полей могут возникнуть принципиально новые эффекты, обязанные своим происхождением именно этим изменениям и не имеющие место в статике. Эффекты эти должны, очевидно, зависеть от производных (исчезающих в статике) соответствующих величин по времени и проявляться тем сильнее, чем больше эти производные. Эксперимент показывает, что такие эффекты действительно возникают. К изучению одного из них, называемого явлением электромагнитной индукции, мы сейчас и переходим[40].