Величина и направление индуктированной ЭДС
Индуктированная ЭДС. возникает в следующих трех случаях:
- когда движущийся проводник пересекает неподвижное магнитное поле или, наоборот, перемещающееся магнитное поле пересекает неподвижный проводник; или когда проводник и магнитное поле, двигаясь в пространстве, перемещаются один относительно другого;
- когда переменное магнитное поле одного проводника, действуя на другой проводник, индуктирует в нем э. д. с. (взаимоиндукция);
- когда изменяющееся магнитное поле какого-либо проводника индуктирует в нем самом э. д. с. (самоиндукция).
Таким образом, всякое изменение во времени величины магнитного потока 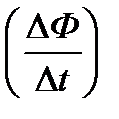 , пронизывающего проводящий контур (виток, рамку), сопровождается появлением в этом проводниковом контуре индуктированной э. д. с. е:
, пронизывающего проводящий контур (виток, рамку), сопровождается появлением в этом проводниковом контуре индуктированной э. д. с. е:
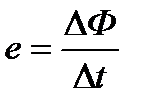
где ΔФ - магнитный поток, пересеченный проводником за промежуток времени Δt.
Величина индуктированной э. д. с. может быть найдена по формуле
где В — величина магнитной индукции, Tл; l - активная длина проводника, м; V - скорость движения проводника, м/сек; α - угол пересечения.
Как было отмечено выше, направление индуктированной э. д. с. зависит от направления движения проводника и от направления магнитного поля.
Для определения направления индуктированной э. д. с. в проводнике, движущемся в магнитном поле, служит «правило правой руки». Оно заключается в следующем: если мысленно расположить правую руку в магнитном поле вдоль проводника так, чтобы магнитные линии, выходящие из северного полюса, входили в ладонь, а большой отогнутый палец совпадал с направлением движения проводника, то четыре вытянутых пальца будут показывать направление э. д. с, индуктированной в проводнике (рис. 94).
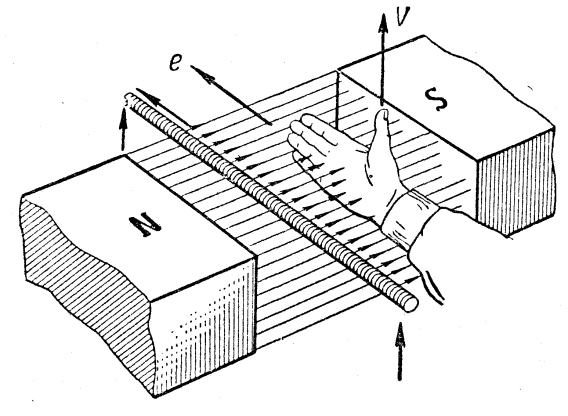
Рис. 94. Определение направления индуктированной э. д. с. в проводнике по «правилу правой руки»
В случаях, когда проводник остается неподвижным, а магнитное поле движется, для определения направления индуктированной э. д. с. следует предположить, что поле остается неподвижным, а проводник движется в сторону, обратную движению поля, и применить также «правило правой руки».
Правило Ленца
В 1834 г. русский академик Э. X. Ленц, известный своими многочисленными исследованиями в области электромагнитных явлений, дал универсальное правило для определения направления индуктированной э. д. с. в проводнике. Это правило, известное как правило Ленца, может быть сформулировано так:
направление индуктированной э. д. с. всегда таково, что вызванный ею ток и его магнитное поле имеют такое направление, что стремятся препятствовать причине, порождающей эту индуктированную э. д. с.
С учетом этого правила можно закон электромагнитной индукции выразить более общей формулой, позволяющей определить не только величину, но и направление индуктированной э. д. с:
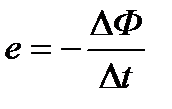
Выражение 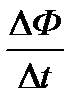 представляет собой среднюю скорость изменения магнитного потока по времени. Чем меньше промежуток времени Δt, тем меньше вышеуказанная э. д. с. отличается от ее действительного значения в данный момент времени.
представляет собой среднюю скорость изменения магнитного потока по времени. Чем меньше промежуток времени Δt, тем меньше вышеуказанная э. д. с. отличается от ее действительного значения в данный момент времени.
Знак минус, стоящий перед выражением  , определяет направление индуктированной э. д. с, т. е. учитывает правило Ленца.
, определяет направление индуктированной э. д. с, т. е. учитывает правило Ленца.
При увеличении магнитного потока выражение 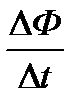 будет положительным, а э. д. с. - отрицательной. В этом и заключается правило Ленца: э. д. с. и созданный ею ток противодействуют причине, которая их вызвала.
будет положительным, а э. д. с. - отрицательной. В этом и заключается правило Ленца: э. д. с. и созданный ею ток противодействуют причине, которая их вызвала.
При равномерном изменении во времени магнитного потока выражение  будет постоянно. Тогда абсолютное значение э. д. с. в проводнике будет равно
будет постоянно. Тогда абсолютное значение э. д. с. в проводнике будет равно
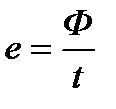
Если катушка состоит из w витков, соединенных между собой последовательно, то индуктированная э.д.с. в ней равняется сумме э.д.с, индуктированных в отдельных витках:
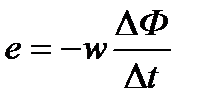
Произведение числа витков катушки на сцепленный с ними магнитный поток называется потокосцеплением катушки и обозначается буквой ψ. Поэтому закон электромагнитной индукции можно записать и в другой форме:
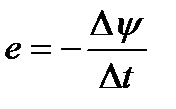
Индуктивность
Магнитный поток, создаваемый током какого-либо витка при отсутствии намагничивающих сред (например, в воздухе), пропорционален величине тока:
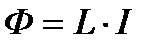
где L - коэффициент пропорциональности, называемый индуктивностью.
Единица измерения индуктивности - генри (Гн): 1 Гн = 103 миллигенри (мГн) = 106 микрогенри (мкГн).
Индуктивность катушек зависит от числа витков, размера и формы катушек.
Цепями с большой индуктивностью являются обмотки генераторов, электродвигателей, трансформаторов, индукционных катушек и т. п. Значительно меньшей индуктивностью обладают прямолинейные проводники.
Короткие прямолинейные проводники, нити ламп накаливания, спирали электронагревательных приборов практически не обладают индуктивностью. На практике часто встречаются случаи, когда нужно изготовить катушку, не обладающую индуктивностью (добавочные сопротивления к электроизмерительным приборам, сопротивление штепсельных реостатов и т. п.). В этом случае применяют бифилярную намотку катушки (рис. 101). Для этого проволоку перед намоткой сгибают вдвое и в таком виде навивают ее. Магнитный поток и индуктивность катушки с бифилярной намоткой равны нулю.
Пусть мы имеем контур, состоящий из одного витка. В этом случае величина э. д. с. самоиндукции будет
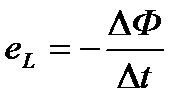
Если ток в контуре изменился на Δi, то магнитный поток изменится на величину ΔФ:
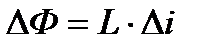
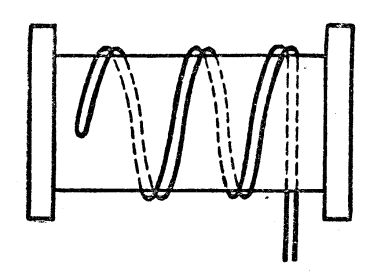
Рис. 101. Бифилярная намотка катушки
Величина э. д. с. самоиндукции, которая возникнет в контуре, будет
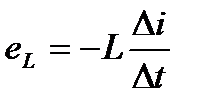
Последнее выражение показывает, что величина э. д. с. самоиндукции зависит от индуктивности контура и скорости изменения тока в контуре.
Отсюда можно дать определение единицы индуктивности - генри: индуктивностью в 1 генри обладает электрическая цепь, в которой при скорости изменения тока на 1 ампер в 1 секунду возникает э. д. с. самоиндукции, равная 1 вольту.
Отдельные витки катушки в общем случае могут пронизываться различными магнитными потоками, поэтому общая э. д. с. катушки будет равна сумме э. д. с. отдельных витков:
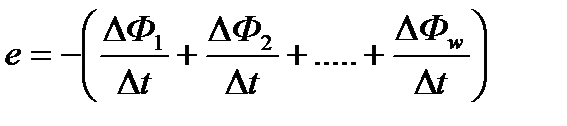
Сумма магнитных потоков, сцепленных со всеми витками катушки, называется потокосцеплением и обозначается буквой ψ:
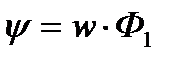
Поэтому выражение индуктивности катушки, состоящей из w витков, в отличие от индуктивности контура с w = 1 будет
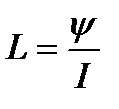
Определим индуктивность кольцевой катушки. Выше нами было найдено выражение для магнитного потока кольцевой катушки:

Так как магнитный поток такой катушки сцеплен со всеми витками, то
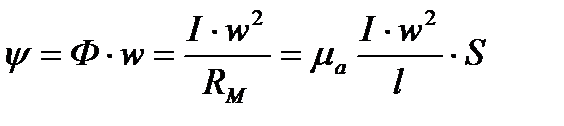
откуда
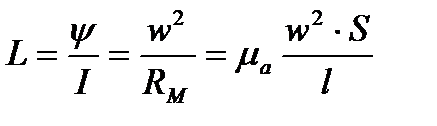
С достаточной для практики точностью ту же самую формулу можно применять для определения индуктивности цилиндрической катушки (соленоида).
Дата добавления: 2017-10-04; просмотров: 4234;











