Вихревое электрическое поле

До сих пор мы не получили ничего физически нового. Закон индукции (4), справедливый для движущегося проводящего контура, однозначно вытекает из выражения (16л17) для силы Лоренца, которая, в свою очередь, является следствием определения магнитного поля (5л16). Если магнитное поле в смысле нашего определения существует, то должен выполняться закон (4). Однако написанная форма этого закона позволяет теоретически обобщить его на значительно более широкий класс явлений, включающий совершенно новый, не имеющий аналогов в статике эффект.

Пусть стационарное магнитное поле B, в котором перемещается исследуемый проводящий контур Г¢, создается другим неподвижным контуром Г с током (рис. 4 а), и пусть контур Г¢ движется поступательно с постоянной скоростью v. В силу неоднородности B магнитный поток, пронизывающий петлю Г¢, при ее движении будет меняться, и в соответствии с (4) в ней возникнет ЭДС индукции e_u . Остановим теперь Г¢, а контур Г начнем двигать (в противоположном направлении) со скоростью – v (рис. 4 б) и посмотрим сначала на происходящее из системы Г. Мы увидим абсолютно то же самое. Действительно, система эта инерциальна, контур Г, возбуждающий магнитное поле, в ней покоится, а исследуемый проводник Г¢ движется относительно него со скоростью v (рис. 4 а). А как будет выглядеть это явление, если вернуться в систему «Земля», где Г¢ неподвижен? Результаты измерений, проведенных в этой системе, могут быть предсказаны теорией относительности путем пересчета по соответствующим формулам результатов, полученных в системе Г. Такой пересчет дает, что результаты эти оказываются, вообще говоря, различными[46]. Однако данные различия становятся сколько-нибудь существенными лишь при скоростях v, сравнимых со скоростью света c. При v << c (а именно такую ситуацию мы и рассматриваем) ими вполне можно пренебречь, так что явления индукции в системах Г и Г¢ должны выглядеть одинаково.

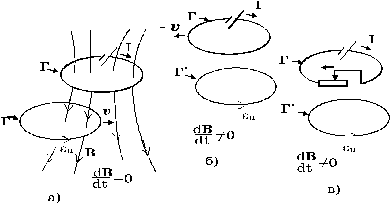Рис. 4.

Итак, ЭДС индукции, возбуждаемая в контуре Г¢, будет определяться формулой (4) и в том случае, когда контур этот неподвижен, а изменение потока F через него вызывается равномерным движением другого контура Г с током, находящегося поблизости. Но в этом случае в месте расположения Г¢ образуется меняющееся со временем магнитное поле B. Такое поле можно получить, если контур Г остановить и просто менять в нем ток (рис. 4 в). Если разделить контуры Г и Г¢ непрозрачной перегородкой, то экспериментатор, исследуя явление индукции в неподвижном контуре Г¢, не сможет определить, чем оно вызвано: равномерным движением контура Г или изменением тока в нем. Естественно ожидать поэтому, что и в данном случае возникающая ЭДС будет по-прежнему определяться формулой (4). Более того, мы предположим, что она останется справедливой и при неравномерном движении контура Г, а также при произвольном изменении тока в нем. Это предположение вполне согласуется с принятой нами точкой зрения близкодействия, согласно которой все «магнитные» явления в данной области пространства должны определяться величиной и направлением магнитного поля (и его производных по времени) в этой области и не зависеть от способа, которым создано это поле. Эксперимент полностью подтверждает наше предположение.

Таким образом, при изменении магнитного потока F, пронизывающего данный контур, вне зависимости от причин, вызывающих это изменение[47], в нем возникает ЭДС индукции, определяемая формулой (4). В такой общей форме закон этот называется законом электромагнитной индукции или законом индукции Фарадея.

Но в чем причина возникновения ЭДС в неподвижном контуре, когда B меняется во времени? На свободные покоящиеся заряды в нем начинает действовать некая сила, которая, если контур замкнут, приводит к появлению индукционного тока. Сила эта, конечно, не электростатического происхождения (некулоновская), причем она действует на заряды пропорционально их величинам. Такие силы мы договорились называть сторонними (именно благодаря этим их свойствам наблюдаемые явления индукции и могут быть охарактеризованы возникающей электродвижущей силой). Значит, вследствие изменения магнитного поля в каких-то участках пространства в них появляется некое поле сторонних сил. Что же это за силы? На первый взгляд может показаться, что они сродни лоренцевым: и те и другие возникают при относительных перемещениях зарядов и токов, возбуждающих магнитное поле. Однако природа их оказывается совершенно различной. Для силы Лоренца необходимо наличие проводящего контура (точнее, движущихся вместе с ним зарядов). Если контур убрать, то вместе с ним исчезнет и сила Лоренца. В мысленно проведенном, т. е. некотором геометрическом контуре, перемещающемся в магнитном поле, сторонней ЭДС не возникает. Строго говоря, мы не можем обнаружить этой ЭДС, иначе как поместив туда движущийся заряд. Никакими другими свойствами, кроме действия на такой заряд, сила Лоренца не обладает.

Совсем иной оказывается ситуация, когда сторонние силы возникают за счет изменения магнитного поля со временем. В этом случае проявляется совершенно новый физический эффект: образуется вихревое электрическое поле, существующее в пространстве независимо от того, есть там проводящий контур, или его нет. Если такой контур имеется и замкнут, то в нем возникает индукционный ток. В противном случае тока, разумеется, нет, но поле все равно существует. Мы можем утверждать это, так как помимо действия на электрический заряд оно обладает еще одним существеннейшим свойством, которое и позволяет его обнаружить, не прибегая к проводящему контуру. Как мы увидим в дальнейшем, изменяясь со временем, оно порождает магнитное поле, причем по точно таким же законам, как и изменяющееся кулоновское[48]. Именно поэтому мы выделяем его из всех остальных сторонних полей и называем электрическим (но не электростатическим!). Поле это – вихревое, непотенциальное, линии его замкнуты, и этим оно принципиально отличается от электростатического. Итак, электрическим мы будем называть теперь поле, могущее порождать по определенным законам (об этом речь впереди) магнитное поле. Такие поля разделяются на два класса: потенциальные электростатические, т. е. созданные каким-то распределением заряда, и непотенциальные вихревые, индуцируемые изменяющимся магнитным полем.

Таким образом, возникающая в соответствии с законом (4) ЭДС индукции может иметь две физически совершенно различные причины:

1) поле стационарно, т. е. 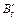= = 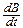0 в каждой точке, но скорость проводящего контура Г (или отдельных его участков) v ¹ 0; при этом природа ЭДС – сила Лоренца 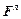и

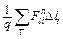e_и = ; (5)

2) контур (не обязательно проводящий) Г неподвижен, т. е. v = 0, но поле меняется, так что 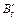¹ 0 хотя бы в каких-то участках пространства; в этом случае причина появления ЭДС – вихревое электрическое поле 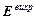и

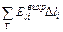e_и = . (6)

Просто удивительно, что два эти физически совершенно различные явления описываются одной и той же формулой (4)!

Закон индукции Фарадея используется для определения единицы магнитного потока. В системе СИ она называется вебером и представляет собой поток через поверхность, ограниченную замкнутой кривой, при равномерном убывании которого до нуля за единицу времени в ней возникает ЭДС индукции e = 1 В:

1 Вб = 1 В×с.

Отсюда может быть установлена единица магнитной индукции. Магнитная индукция равна единице, если через перпендикулярную площадку единичной площади она создает поток, равный единице. В системе СИ[49]

1 Тл = 1 Вб/м2.