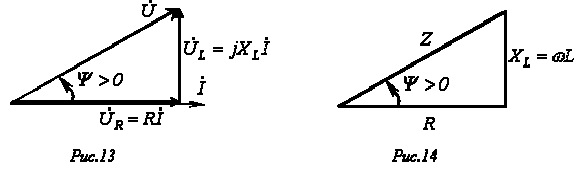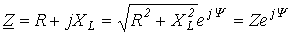Действующее значение синусоидальных ЭДС, напряжений и токов
В соответствии с выражением (3) для действующего значения синусоидального тока запишем:
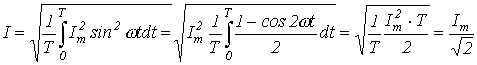 .
.
Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в 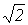 раз:
раз:
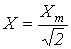 . .
| (10) |
Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения
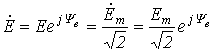 .
.
Литература
1. Основытеории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?
2. Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?
3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?
4. Для заданных синусоидальных функций ЭДС и тока 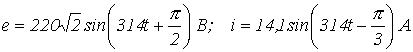 записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.
записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.
5. На рис. 5 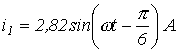 , а
, а 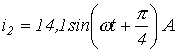 . Определить
. Определить 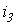 .
.
Ответ: 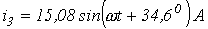
| Теория / ТОЭ / Лекция N 4. Элементы цепи синусоидального тока. Векторные диаграммы и комплексные соотношения для них. |
1. Резистор
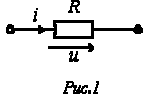
Идеальный резистивный элемент не обладает ни индуктивностью, ни емкостью. Если к нему приложить синусоидальное напряжение 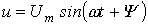 (см. рис. 1), то ток i через него будет равен (см. рис. 1), то ток i через него будет равен
Из (1) вытекает:
Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам: - разделим первый из них на второй: или
Полученный результат показывает, что отношение двух комплексов есть вещественная константа. Следовательно, соответствующие им векторы напряжения и тока (см. рис. 3) совпадают по направлению.
Конденсатор Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение
Из (3) вытекает:
Введенный параметр Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам: - разделим первый из них на второй: или
3. Катушка индуктивности Идеальный индуктивный элемент не обладает ни активным сопротивлением, ни емкостью. Пусть протекающий через него ток (см. рис. 8) определяется выражением
Полученный результат показывает, что напряжение на катушке индуктивности опережает по фазе ток на Из (5) вытекает:
Введенный параметр Переходя от синусоидальных функций напряжения и тока к соответствующим комплексам: разделим первый из них на второй: или
сопротивление катушки индуктивности. Умножение на
. 4. Последовательное соединение резистивного и индуктивного элементов
Уравнению (7) можно поставить в соответствие соотношение
графически может быть представлено треугольником сопротивлений (см. рис. 14), который подобен треугольнику напряжений.
Дата добавления: 2016-06-29; просмотров: 2534; |

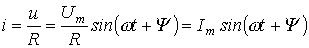 .
.
 Соотношение (1) показывает, что ток имеет ту же начальную фазу, что и напряжение. Таким образом, если на входе двухлучевого осциллографа подать сигналы u и i, то соответствующие им синусоиды на его экране будут проходить (см. рис. 2) через нуль одновременно, т.е. на резисторе напряжение и ток совпадают по фазе.
Соотношение (1) показывает, что ток имеет ту же начальную фазу, что и напряжение. Таким образом, если на входе двухлучевого осциллографа подать сигналы u и i, то соответствующие им синусоиды на его экране будут проходить (см. рис. 2) через нуль одновременно, т.е. на резисторе напряжение и ток совпадают по фазе.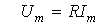 ;
;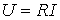 .
.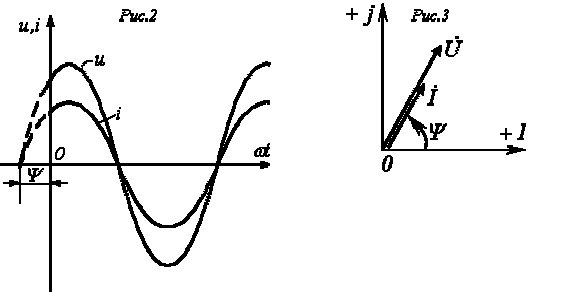
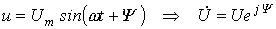 ;
;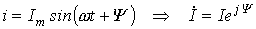 ,
,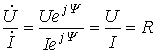
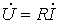 .
.
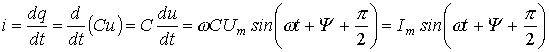 .
.
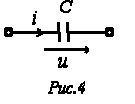 Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на
Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на 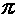 /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране будет иметь место картинка, соответствующая рис. 5.
/2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране будет иметь место картинка, соответствующая рис. 5.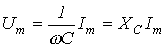 ;
;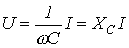 .
.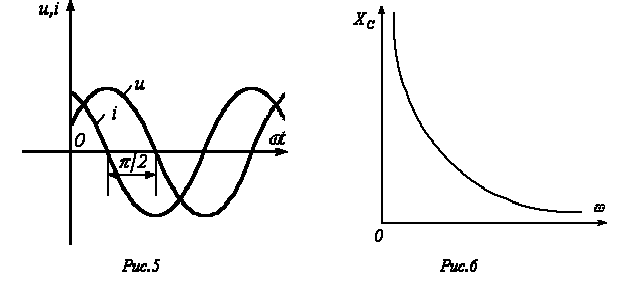
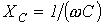 называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление,
называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление, 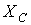 имеет размерность Ом. Однако в отличие от R данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при
имеет размерность Ом. Однако в отличие от R данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при 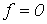 конденсатор представляет разрыв для тока, а при
конденсатор представляет разрыв для тока, а при 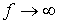
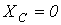 .
.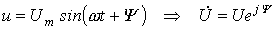 ;
;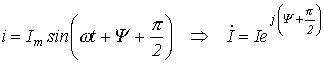 ,
,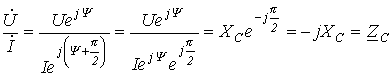
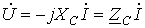 .
.
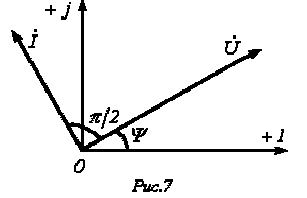 В последнем соотношении
В последнем соотношении  - комплексное сопротивление конденсатора. Умножение на
- комплексное сопротивление конденсатора. Умножение на 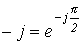 соответствует повороту вектора на угол
соответствует повороту вектора на угол 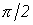 по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.
по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.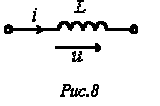
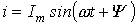 . Тогда для напряжения на зажимах катушки индуктивности можно записать
. Тогда для напряжения на зажимах катушки индуктивности можно записать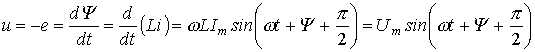 .
.
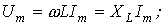
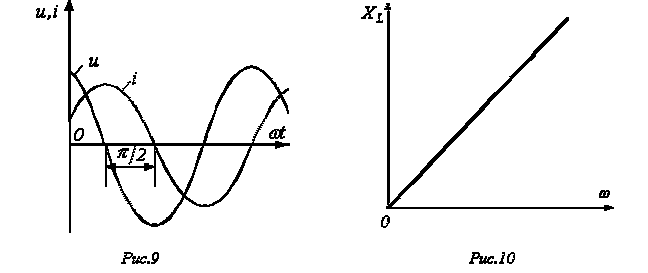
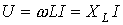 .
.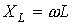 называют реактивным индуктивным сопротивлением катушки;его размерность – Ом. Как и у емкостного элемента этот параметр является функцией частоты. Однако в данном случае эта зависимость имеет линейный характер, что иллюстрирует рис. 10. Из рис. 10 вытекает, что при
называют реактивным индуктивным сопротивлением катушки;его размерность – Ом. Как и у емкостного элемента этот параметр является функцией частоты. Однако в данном случае эта зависимость имеет линейный характер, что иллюстрирует рис. 10. Из рис. 10 вытекает, что при 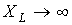 .
.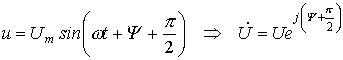 ;
;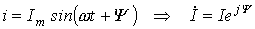 ,
,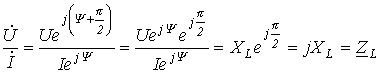
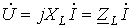 .
.
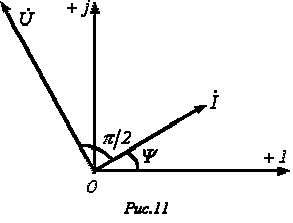 В полученном соотношении
В полученном соотношении 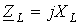 - комплексное
- комплексное соответствует повороту вектора на угол
соответствует повороту вектора на угол 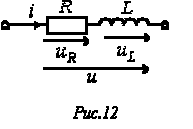 Пусть в ветви на рис. 12
Пусть в ветви на рис. 12 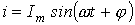 . Тогда
. Тогда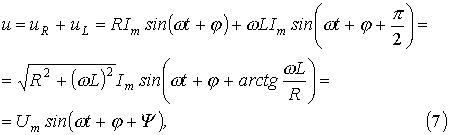 где
где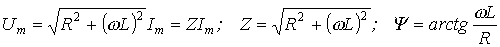 , причем пределы изменения
, причем пределы изменения 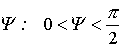 .
.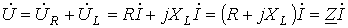 ,
,