Исключения из «правила потока»

При вычислении ЭДС индукции по формуле (4) необходимо иметь в виду, что формальное ее использование может иногда приводить к ошибкам. В качестве иллюстрации рассмотрим два примера.

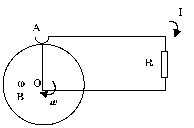Рис. 5.

Пусть в перпендикулярном плоскости чертежа поле B вращается с угловой скоростью w проводящий диск (рис. 5). Участок OA диска между скользящими контактами A и осью O входит в состав замкнутой цепи OAR, поток Ф через которую при вращении диска не меняется. Однако движущиеся вместе с диском заряды будут испытывать силу Лоренца и в контуре OAR возникнет в соответствии с (5) (где суммирование достаточно распространить лишь на участок OA) ЭДС индукции и потечет ток.

Пример обратной ситуации (опять же в стационарном магнитном поле) представлен на рис. 6. Две плоские проводящие пластины специальной формы, расположенные в одной плоскости и обращенные друг к другу своими выпуклыми очень пологими (большого радиуса кривизны) кромками, контактируют в точке A, образуя изображенный на рисунке замкнутый контур с гальванометром G. При небольшом покачивании пластин в плоскости чертежа (перпендикулярной направлению магнитного поля) точка контакта будет сильно смещаться вдоль соприкасающихся кромок пластин, приводя к значительному изменению площади контура и пронизывающего его магнитного потока. Стало быть, DF здесь есть, а индукционного тока, как нетрудно понять, практически не возникает. Ведь при таких манипуляциях любой участок пластин перемещений почти не совершает (для этого мы и выбираем их кромки в виде дуг окружностей большого радиуса) и сила Лоренца везде (а следовательно, и возникающая ЭДС) близка к нулю.

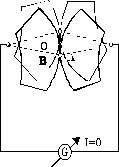Рис. 6.

Приведенные примеры показывают, что «правило потока» (4) иногда не выполняется. Из них явствует также, что это может произойти, когда природа ЭДС – сила Лоренца, а цепь составлена из проводников сложной формы, причем скорости участков самого контура и частиц, образующих этот контур, не совпадают. Другими словами, чтобы закон (4) не имел исключений, нужно потребовать, чтобы материал проводящего контура, фигурирующего в (4), не менялся. Впрочем, верное физическое содержание этого закона – в выражениях (5) и (6), применение которых гарантирует от недоразумений.

Правило Ленца

Если проводящий контур, магнитный поток через который меняется, замкнут, то в нем возникает индукционный ток, возбуждающий собственное поле. Поскольку поле это составляет с током I правовинтовую систему, а сам ток с изменением внешнего магнитного потока – систему левовинтовую, справедливо следующее правило Ленца. Индукционный ток всегда имеет такое направление, что создаваемый им магнитный поток Ф_соб препятствует изменению внешнего потока, вызвавшего этот ток. Это значит, что если внешний поток убывает, то собственный, препятствуя этому, должен быть направлен в ту же сторону, если же он возрастает, то Ф_соб направлен навстречу внешнему.

Правило Ленца позволяет сразу находить направление индукционного тока, не прибегая к последовательному применению правил левого и правого винтов.

Правило Ленца может быть получено и непосредственно из энергетических соображений. Рассмотрим, например, два замкнутых проводящих контура, индуктивно связанных друг с другом, т. е. расположенных таким образом, что магнитный поток первого контура частично или полностью пронизывает второй и наоборот. Пусть ток, скажем, в первом контуре случайно увеличился на очень малую величину DI₁ (или появился, если его там не было). Тотчас же возникает нарастающий магнитный поток F₁ , пронизывающий второй контур, и в нем появится индукционный ток. Если бы собственный магнитный поток F₂ этого контура (а он тоже, очевидно, будет нарастающим) вопреки правилу Ленца не препятствовал, а способствовал бы увеличению Ф₁, то возникшая флуктуация тока в первом контуре начала бы расти: ведь возрастающий поток F₂ опять же в нарушение правила Ленца вызывал бы возрастание F₁, а следовательно, и DI₁. Возник бы лавинный процесс неограниченного роста токов в обоих контурах, что противоречит принципу сохранения энергии, да и здравому смыслу вообще.

Самоиндукция

Изменяющийся магнитный поток, пронизывающий контур и вызывающий появление ЭДС индукции, не обязательно должен быть внешним. Если в контуре течет ток (индукционный или созданный включенной в него сторонней ЭДС), то имеется собственный магнитный поток через этот контур, который при изменении будет возбуждать в нем e_u в точности по закону (4). Ведь каждый участок контура находится в поле остальных, которое является для него внешним, а потому и ЭДС, возникающая в нем, не зависит от того, чем создано это поле: остальными участками контура или другими токами.

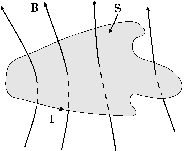Рис. 7.

Рассмотрим уединенный замкнутый проводник произвольной формы (рис. 7) и пустим по нему постоянный ток I, включив в цепь стороннюю ЭДС (на рис. не изображена). Можно показать, что распределение тока по сечению проводника не зависит от его силы, а определяется лишь геометрией и характером изменения проводимости (если она непостоянна) внутри объема проводника[50]. Это значит, что при удвоении тока удваивается его плотность (не меняясь по направлению) в каждой точке внутри проводника и, стало быть, по закону Био – Савара (8л16) возбуждаемое им в окружающем пространстве магнитное поле. Удвоится оно и в точках произвольной поверхности, опирающейся на контур рассматриваемого проводника, и, следовательно, поток через нее Ф_соб тоже удвоится. Таким образом, поток этот оказывается пропорциональным току, текущему по контуру:

Ф_соб = LI, (7)

где постоянный коэффициент L, зависящий от геометрии проводника и распределения внутри него удельной проводимости, называется индуктивностью или коэффициентом самоиндукции проводника.

Из определения L следует его единица – генри (в СИ). Очевидно,

1 Гн =1 Вб/А,

т. е. индуктивность контура равна 1 Гн, если ток в 1 А создает поток через него в 1 Вб.

Найдем в качестве примера индуктивность длинного соленоида. Для этого натянем на контур тока, т. е. на все его N витков, образующих винтовую линию, одну поверхность, площадь которой, очевидно, будет равна NS (где S – площадь витка). Поток вектора B через нее согласно (12л17)

F_соб = BNS = = ,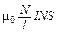

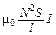где l – длина соленоида, откуда индуктивность его

L = 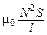. (8)

Отсюда получают единицу магнитной постоянной m₀ , которая, как нетрудно видеть, оказывается равной Гн/м.

Замечание. Приведенное выше определение индуктивности (7) нуждается в уточнении. Дело в том, что из него неясно, через какую точно поверхность считается поток Ф_соб . Трудность связана с тем, что индуктивность бесконечно тонкого проводника, через который поток, а точнее контур поверхности для расчета потока, определяется однозначно, физического смысла не имеет: вблизи такого проводника поле, а вместе с ним и поток стремятся к бесконечности при сколь угодно малом токе I[51]. Поэтому определение (7) необходимо сразу распространять на случай проводника конечного сечения, т. е. достаточно «толстого», внутри которого можно провести различные контуры. Таким образом, при одном и том же токе I в зависимости от выбранного контура (расположенного в толще нашего проводника) его будут пронизывать, вообще говоря, несколько различные (а если проводник достаточно толстый – то существенно различные) потоки, так что коэффициент L оказывается неопределенным. Поэтому уточним определение (7) и будем понимать в нем под Ф_соб средний магнитный поток, пронизывающий рассматриваемый проводник. Для его расчета нужно разбить циркулирующий ток на квазилинейные трубки, в пределах любого сечения которых B » const, посчитать поток (созданный всеми трубками) через контур каждой такой трубки и результаты усреднить по всем контурам.

Отсюда понятно, что вычисление индуктивности замкнутого проводника произвольной формы и сечения представляет собой весьма сложную задачу и требует предварительного расчета распределения в нем токов. В рассмотренном выше примере с индуктивностью соленоида мы легко нашли L только потому, что распределение токов фактически уже было задано.

Рассмотрим теперь процессы, происходящие в контуре при изменении тока в нем. Если ток в контуре меняется, а контур не деформируется (т. е. L = const), то в соответствии с (4) и (7) в нем возникает так называемая ЭДС самоиндукции

e_си = 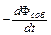= = 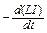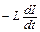, (9)

где знак минус означает, что e_си направлена навстречу току, если он возрастает, и по току, если он убывает. В более общем случае деформируемого контура в выражении для e_си появляется член I 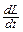, характеризующий вклад в ЭДС этой деформации. Мы, однако, такие случаи рассматривать не будем.

Из (9) следует, что при замыкании цепи постоянного тока с индуктивностью ток достигает своего установившегося значения не мгновенно, а с некоторым опозданием. Возникающая сразу же после замыкания встречная ЭДС самоиндукции мешает нарастанию тока и затягивает процесс. При размыкании же цепи, как только ток начинает падать, появившаяся e_си поддерживает его. Если цепь разомкнуть быстро, то 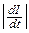, а следовательно e_си , может достигнуть огромных значений. Это приведет к появлению больших напряжений в месте разрыва цепи и проскакиванию там искры, что позволит току все-таки продлиться некоторое время (ведь мгновенно же он не может исчезнуть!)[52].

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ